Angular Momentum

Recall that the concept of linear momentum  and the principle of conservation of linear momentum are extremely powerful tools. They allow us to predict the outcome of, say, a collision of two cars without knowing the details of the collision. Here we begin a discussion of the angular counterpart of , winding up in Section 11-11 with the angular counterpart of the conservation principle.

Figure 11-12 shows a particle of mass m with linear momentum  as it passes through point A in an xy plane. The angular momentum  of this particle with respect to the origin O is a vector quantity defined as

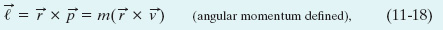
where  is the position vector of the particle with respect to O. As the particle moves relative to O in the direction of its momentum , position vector  rotates around O. Note carefully that to have angular momentum about O, the particle does not itself have to rotate around O. Comparison of Eqs. 11-14 and 11-18 shows that angular momentum bears the same relation to linear momentum that torque does to force. The SI unit of angular momentum is the kilogram-meter-squared per second (kg · m²/s), equivalent to the joule-second (J · s).

To find the direction of the angular momentum vector  in Fig. 11-12, we slide the vector  until its tail is at the origin O. Then we use the right-hand rule for vector products, sweeping the fingers from  into . The outstretched thumb then shows that the direction of  is in the positive direction of the z axis in Fig. 11-12. This positive direction is consistent with the counterclockwise rotation of position vector  about the z axis, as the particle moves. (A negative direction of  would be consistent with a clockwise rotation of  about the z axis.)

To find the magnitude of , we use the general result of Eq. 3-27 to write

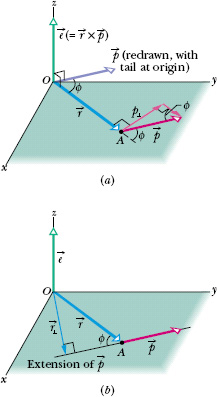
Fig. 11-12   Defining angular momentum. A particle passing through point A has linear momentum , with the vector  lying in an xy plane. The particle has angular momentum  with respect to the origin O. By the right-hand rule, the angular momentum vector points in the positive direction of z. (a) The magnitude of  is given by . (b) The magnitude of  is also given by .

where  is the smaller angle between  and  when these two vectors are tail to tail. From Fig. 11-12a, we see that Eq. 11-19 can be rewritten as

where p_⊥ is the component of  perpendicular to  and v_⊥ is the component of  perpendicular to . From Fig. 11-12b, we see that Eq. 11-19 can also be rewritten as

where r_⊥ is the perpendicular distance between O and the extension of .

Just as is true for torque, angular momentum has meaning only with respect to a specified origin. Moreover, if the particle in Fig. 11-12 did not lie in the xy plane, or if the linear momentum  of the particle did not also lie in that plane, the angular momentum  would not be parallel to the z axis. The direction of the angular momentum vector is always perpendicular to the plane formed by the position and linear momentum vectors  and .

CHECK POINT 4    In part a of the figure, particles 1 and 2 move around point O in opposite directions, in circles with radii 2 m and 4 m. In part b, particles 3 and 4 travel in the same direction, along straight lines at perpendicular distances of 4 m and 2 m from point O. Particle 5 moves directly away from O. All five particles have the same mass and the same constant speed. (a) Rank the particles according to the magnitudes of their angular momentum about point O, greatest first. (b) Which particles have negative angular momentum about point O?

Sample Problem 11-4

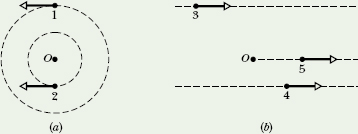
Figure 11-13 shows an overhead view of two particles moving at constant momentum along horizontal paths. Particle 1, with momentum magnitude p₁ = 5.0 kg · m/s, has position vector  and will pass 2.0 m from point O. Particle 2, with momentum magnitude p₂ = 2.0 kg · m/s, has position vector  and will pass 4.0 m from point O. What are the magnitude and direction of the net angular momentum  about point O of the two-particle system?

Solution: The Key Idea here is that to find , we can first find the individual angular momenta ₁ and ₂ and then add them. To evaluate their magnitudes, we can use any one of Eqs. 11-18 through 11-21. However, Eq. 11-21 is easiest, because we are given the perpendicular distances r_1⊥ (= 2.0 m) and r_2⊥ (= 4.0 m) and the momentum magnitudes p₁ and p₂. We are not given all the values required for the variables in the other equations.

For particle 1, Eq. 11-21 yields

ℓ₁ = r_⊥1p₁ = (2.0 m)(5.0 kg · m/s)
= 10 kg · m²/s.

To find the direction of vector , we use Eq. 11-18 and the right-hand rule for vector products. For , the vector product is out of the page, perpendicular to the plane of Fig. 11-13. This is the positive direction, consistent with the counterclockwise rotation of the particle’s position vector  around O as particle 1 moves. Thus, the angular momentum vector for particle 1 is

Fig. 11-13   Two particles pass near point O.

ℓ₁ = +10 kg · m²/s.

Similarly, the magnitude of ₂ is

ℓ₂ = r_⊥2p₂ = (4.0 m)(2.0 kg · m/s)
   = 8.0 kg · m²/s,

and the vector product  is into the page, which is the negative direction, consistent with the clockwise rotation of  around O as particle 2 moves. Thus, the angular momentum vector for particle 2 is

ℓ₂ = −8.0 kg · m²/s.

The net angular momentum for the two-particle system is then

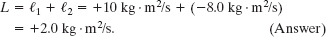
The plus sign means that the system’s net angular momentum about point O is out of the page.