The Forces of Rolling

Friction and Rolling

If a wheel rolls at constant speed, as in Fig. 11-3, it has no tendency to slide at the point of contact P, and thus no frictional force acts there. However, if a net force acts on the rolling wheel to speed it up or to slow it, then that net force causes acceleration  of the center of mass along the direction of travel. It also causes the wheel to rotate faster or slower, which means it causes an angular acceleration α. These accelerations tend to make the wheel slide at P. Thus, a frictional force must act on the wheel at P to oppose that tendency.

If the wheel does not slide, the force is a static frictional force  and the motion is smooth rolling. We can then relate the magnitudes of the linear acceleration  and the angular acceleration α by differentiating Eq. 11-2 with respect to time (with R held constant). On the left side, dv_com/dt is a_com, and on the right side dω/dt is α. So, for smooth rolling we have

If the wheel does slide when the net force acts on it, the frictional force that acts at P in Fig. 11-3 is a kinetic frictional force . The motion then is not smooth rolling, and Eq. 11-6 does not apply to the motion. In this chapter we discuss only smooth rolling motion.

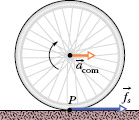
Fig. 11-7   A wheel rolls horizontally without sliding while accelerating with linear acceleration  . A static frictional force  acts on the wheel at P, opposing its tendency to slide.

Figure 11-7 shows an example in which a wheel is being made to rotate faster while rolling to the right along a flat surface, as on a bicycle at the start of a race. The faster rotation tends to make the bottom of the wheel slide to the left at point P. A frictional force at P, directed to the right, opposes this tendency to slide. If the wheel does not slide, that frictional force is a static frictional force  (as shown), the motion is smooth rolling, and Eq. 11-6 applies to the motion.(Without friction, bicycle races would be stationary and very boring.)

If the wheel in Fig. 11-7 were made to rotate slower, as on a slowing bicycle, we would change the figure in two ways: The directions of the center-of-mass acceleration  and the frictional force  at point P would now be to the left.

Rolling Down a Ramp

Figure 11-8 shows a round uniform body of mass M and radius R rolling smoothly down a ramp at angle θ, along an x axis. We want to find an expression for the body’s acceleration a_com,x down the ramp. We do this by using Newton’s second law in both its linear version (F_net = Ma) and its angular version (τ_net = Iα).

We start by drawing the forces on the body as shown in Fig. 11-8:

1.  The gravitational force  on the body is directed downward. The tail of the vector is placed at the center of mass of the body. The component along the ramp is F_g sin θ, which is equal to Mg sin θ.

2.  A normal force  is perpendicular to the ramp. It acts at the point of contact P, but in Fig. 11-8 the vector has been shifted along its direction until its tail is at the body’s center of mass.

3.  A static frictional force  acts at the point of contact P and is directed up the ramp. (Do you see why? If the body were to slide at P, it would slide down the ramp. Thus, the frictional force opposing the sliding must be up the ramp.)

We can write Newton’s second law for components along the x axis in Fig. 11-8 (F _net,x = ma_x) as

This equation contains two unknowns, f_s and a_com,x. (We should not assume that f_s is at its maximum value f_s,max. All we know is that the value of f_s is just right for the body to roll smoothly down the ramp, without sliding.)

We now wish to apply Newton’s second law in angular form to the body’s rotation about its center of mass. First, we shall use Eq. 10-41 (τ = r_⊥F) to write the torques on the body about that point. The frictional force  has moment arm R and thus produces a torque Rf_s, which is positive because it tends to rotate the body counterclockwise in Fig. 11-8. Forces  and  have zero moment arms about the center of mass and thus produce zero torques. So we can write the angular form of Newton’s second law (τ_net = Iα) about an axis through the body’s center of mass as

This equation contains two unknowns, f_s and α.

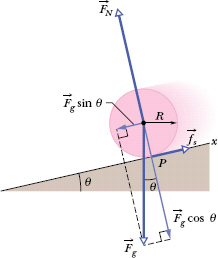
Fig. 11-8   A round uniform body of radius R rolls down a ramp. The forces that act on it are the gravitational force , a normal force , and a frictional force  pointing up the ramp. (For clarity, vector  has been shifted in the direction it points until its tail is at the center of the body.)

Because the body is rolling smoothly, we can use Eq. 11-6 (a_com = αR) to relate the unknowns a_com,x and α. But we must be cautious because here a_com,x is negative (in the negative direction of the x axis) and α is positive (counterclockwise). Thus we substitute −a_com,x/R for α in Eq. 11-8. Then, solving for f_s, we obtain

Substituting the right side of Eq. 11-9 for f_s in Eq. 11-7, we then find

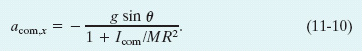
We can use this equation to find the linear acceleration a_com,x of any body rolling along an incline of angle θ with the horizontal.

CHECKPOINT 2   Disks A and B are identical and roll across a floor with equal speeds. Then disk A rolls up an incline, reaching a maximum height h, and disk B moves up an incline that is identical except that it is frictionless. Is the maximum height reached by disk B greater than, less than, or equal to h?

Sample Problem 11-2

A uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ = 30.0° (Fig. 11-8).

(a) The ball descends a vertical height h = 1.20 m to reach the bottom of the ramp. What is its speed at the bottom?

Solution: One Key Idea here is that we can relate the ball’s speed at the bottom to its kinetic energy K_f there. A second Key Idea is that the mechanical energy E of the ball–Earth system is conserved as the ball rolls down the ramp. The reason is that the only force doing work on the ball is the gravitational force, a conservative force. The normal force on the ball from the ramp does zero work because it is perpendicular to the ball’s path. The frictional force on the ball from the ramp does not transfer any energy to thermal energy because the ball does not slide (it rolls smoothly).

Therefore, we can write the conservation of mechanical energy (E_f = E_i) as

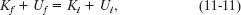
where subscripts f and i refer to the final values (at the bottom) and initial values (at rest), respectively. The gravitational potential energy is initially U_i = Mgh (where M is the ball’s mass) and finally U_f = 0. The kinetic energy is initially K_i = 0. For the final kinetic energy K_f, we need a third Key Idea: Because the ball rolls, the kinetic energy involves both translation and rotation, so we include them both by using the right side of Eq. 11-5. Substituting all these expressions into Eq. 11-11 gives us

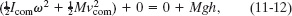
where I_com is the ball’s rotational inertia about an axis through its center of mass, v_com is the requested speed at the bottom, and ω is the angular speed there.

Because the ball rolls smoothly, we can use Eq. 11-2 to substitute v_com/R for ω to reduce the unknowns in Eq. 11-12. Doing so, substituting  for I_com (from Table 10-2f), and then solving for v_com give us

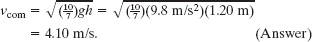
Note that the answer does not depend on the mass M or radius R of the ball.

(b) What are the magnitude and direction of the frictional force on the ball as it rolls down the ramp?

Solution: The Key Idea here is that, because the ball rolls smoothly, Eq. 11-9 gives the frictional force on the ball. However, first we need the ball’s acceleration a_com,x from Eq. 11-10:

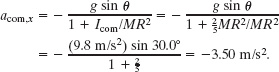
Note that we needed neither mass M nor radius R to find a_com,x. Thus, any size ball with any uniform mass would have this acceleration down a 30.0° ramp, provided the ball rolls smoothly.

We can now solve Eq. 11-9 as

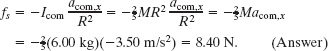
Note that we needed mass M but not radius R. Thus, the frictional force on any 6.00 kg ball rolling smoothly down a 30.0° ramp would be 8.40 N regardless of the ball’s radius.