When two bodies collide, the impulse between them determines the directions in which they then travel. In particular, when the collision is not head-on, the bodies do not end up traveling along their initial axis. For such two-dimensional collisions in a closed, isolated system, the total linear momentum must still be conserved:

If the collision is also elastic (a special case), then the total kinetic energy is also conserved:

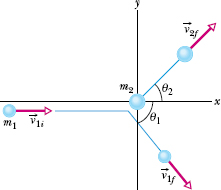
Fig. 9-22 An elastic collision between two bodies in which the collision is not head-on. The body with mass m2 (the target) is initially at rest.
Equation 9-77 is often more useful for analyzing a two-dimensional collision if we write it in terms of components on an xy coordinate system. For example, Fig. 9-22 shows a glancing collision (it is not head-on) between a projectile body and a target body initially at rest. The impulses between the bodies have sent the bodies off at angles θ1 and θ2 to the x axis, along which the projectile initially traveled. In this situation we would rewrite Eq. 9-77 for components along the x axis as
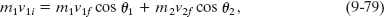
and along the y axis as
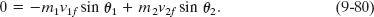
We can also write Eq. 9-78 (for the special case of an elastic collision) in terms of speeds:
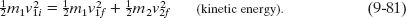
Equations 9-79 to 9-81 contain seven variables: two masses, m1 and m2; three speeds, v1i, v1f, and v2f; and two angles, θ1 and θ2. If we know any four of these quantities, we can solve the three equations for the remaining three quantities.
![]() CHECKPOINT 11 In Fig. 9-22, suppose that the projectile has an initial momentum of 6 kg · m/s, a final x component of momentum of 4 kg · m/s, and a final y component of momentum of −3 kg · m/s. For the target, what then are (a) the final x component of momentum and (b) the final y component of momentum?
CHECKPOINT 11 In Fig. 9-22, suppose that the projectile has an initial momentum of 6 kg · m/s, a final x component of momentum of 4 kg · m/s, and a final y component of momentum of −3 kg · m/s. For the target, what then are (a) the final x component of momentum and (b) the final y component of momentum?
9-12 Systems with Varying Mass: A Rocket
In the systems we have dealt with so far, we have assumed that the total mass of the system remains constant. Sometimes, as in a rocket, it does not. Most of the mass of a rocket on its launching pad is fuel, all of which will eventually be burned and ejected from the nozzle of the rocket engine.
We handle the variation of the mass of the rocket as the rocket accelerates by applying Newton’s second law, not to the rocket alone but to the rocket and its ejected combustion products taken together. The mass of this system does not change as the rocket accelerates.
Finding the Acceleration
Assume that we are at rest relative to an inertial reference frame, watching a rocket accelerate through deep space with no gravitational or atmospheric drag forces acting on it. For this one-dimensional motion, let M be the mass of the rocket and v its velocity at an arbitrary time t (see Fig. 9-23a).
Figure 9-23b shows how things stand a time interval dt later. The rocket now has velocity v + dv and mass M + dM, where the change in mass dM is a negative quantity. The exhaust products released by the rocket during interval dt have mass −dM and velocity U relative to our inertial reference frame.
Our system consists of the rocket and the exhaust products released during interval dt. The system is closed and isolated, so the linear momentum of the system must be conserved during dt; that is,

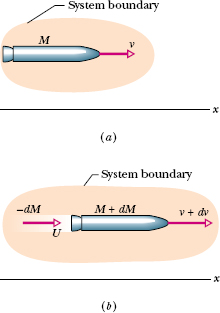
Fig. 9-23 (a) An accelerating rocket of mass M at time t, as seen from an inertial reference frame. (b) The same but at time t + dt. The exhaust products released during interval dt are shown.
where the subscripts i and f indicate the values at the beginning and end of time interval dt. We can rewrite Eq. 9-82 as
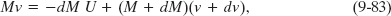
where the first term on the right is the linear momentum of the exhaust products released during interval dt and the second term is the linear momentum of the rocket at the end of interval dt.
We can simplify Eq. 9-83 by using the relative speed vrel between the rocket and the exhaust products, which is related to the velocities relative to the frame with
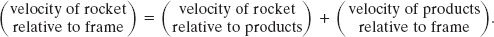
In symbols, this means
(v + dv) = vrel + U,
or

Substituting this result for U into Eq. 9-83 yields, with a little algebra,

Dividing each side by dt gives us

We replace dM/dt (the rate at which the rocket loses mass) by −R, where R is the (positive) mass rate of fuel consumption, and we recognize that dv/dt is the acceleration of the rocket. With these changes, Eq. 9-86 becomes

Equation 9-87 holds at any instant, with the mass M, the fuel consumption rate R, and the acceleration a evaluated at that instant.
Note the left side of Eq. 9-87 has the dimensions of force (kg/s · m/s = kg · m/s2 = N) and depends only on design characteristics of the rocket engine—namely, the rate R at which it consumes fuel mass and the speed vrel with which that mass is ejected relative to the rocket. We call this term Rvrel the thrust of the rocket engine and represent it with T. Newton’s second law emerges clearly if we write Eq. 9-87 as T = Ma, in which a is the acceleration of the rocket at the time that its mass is M.
Finding the Velocity
How will the velocity of a rocket change as it consumes its fuel? From Eq. 9-85 we have
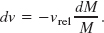
Integrating leads to
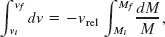
in which Mi is the initial mass of the rocket and Mf its final mass. Evaluating the integrals then gives
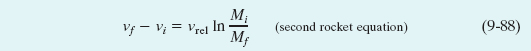
for the increase in the speed of the rocket during the change in mass from Mi to Mf. (The symbol “ln” in Eq. 9-88 means the natural logarithm.) We see here the advantage of multistage rockets, in which Mf is reduced by discarding successive stages when their fuel is depleted. An ideal rocket would reach its destination with only its payload remaining.
Leave a Reply