In this section, we discuss only a single particle instead of a system of particles, in order to define two important quantities. Then in Section 9-5, we extend those definitions to systems of many particles.
The first definition concerns a familiar word—momentum—that has several meanings in everyday language but only a single precise meaning in physics and engineering. The linear momentum of a particle is a vector quantity 
that is defined as
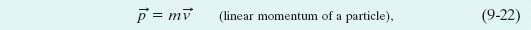
in which m is the mass of the particle and 
is its velocity. (The adjective linear is often dropped, but it serves to distinguish from angular momentum, which is introduced in Chapter 11 and which is associated with rotation.) Since m is always a positive scalar quantity, Eq. 9-22 tells us that and have the same direction. From Eq. 9-22, the SI unit for momentum is the kilogram-meter per second (kg · m/s).
Newton expressed his second law of motion in terms of momentum:
The time rate of change of the momentum of a particle is equal to the net force acting on the particle and is in the direction of that force.
In equation form this becomes
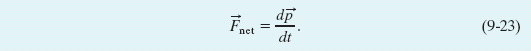
In words, Eq. 9-23 says that the net external force 
on a particle changes the particle’s linear momentum . Conversely, the linear momentum can be changed only by a net external force. If there is no net external force, cannot change. As we shall see in Section 9-7, this last fact can be an extremely powerful tool in solving problems.
Manipulating Eq. 9-23 by substituting for from Eq. 9-22 gives, for constant mass m,
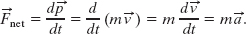
Thus, the relations 
are equivalent expressions of Newton’s second law of motion for a particle.
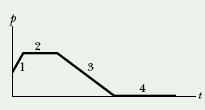
CHECKPOINT 3 The figure gives the magnitude p of the linear momentum versus time t for a particle moving along an axis. A force directed along the axis acts on the particle. (a) Rank the four regions indicated according to the magnitude of the force, greatest first. (b) In which region is the particle slowing?
Leave a Reply