We now have discussed several situations in which energy is transferred to or from objects and systems, much like money is transferred between accounts. In each situation we assume that the energy that was involved could always be accounted for; that is, energy could not magically appear or disappear. In more formal language, we assumed (correctly) that energy obeys a law called the law of conservation of energy, which is concerned with the total energy E of a system. That total is the sum of the system’s mechanical energy, thermal energy, and any type of internal energy in addition to thermal energy. (We have not yet discussed other types of internal energy.) The law states that

Fig. 8-15 To descend, the rock climber must transfer energy from the gravitational potential energy of a system consisting of her, her gear, and Earth. She has wrapped the rope around metal rings so that the rope rubs against the rings. This allows most of the transferred energy to go to the thermal energy of the rope and rings rather than to her kinetic energy.
![]() The total energy E of a system can change only by amounts of energy that are transferred to or from the system.
The total energy E of a system can change only by amounts of energy that are transferred to or from the system.
The only type of energy transfer that we have considered is work W done on a system. Thus, for us at this point, this law states that
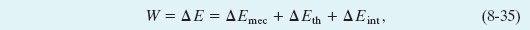
where ΔEmec is any change in the mechanical energy of the system, ΔEth is any change in the thermal energy of the system, and ΔEint is any change in any other type of internal energy of the system. Included in ΔEmec are changes ΔK in kinetic energy and changes ΔU in potential energy (elastic, gravitational, or any other type we might find).
This law of conservation of energy is not something we have derived from basic physics principles. Rather, it is a law based on countless experiments. Scientists and engineers have never found an exception to it.
Isolated System
If a system is isolated from its environment, there can be no energy transfers to or from it. For that case, the law of conservation of energy states:
![]() The total energy E of an isolated system cannot change.
The total energy E of an isolated system cannot change.
Many energy transfers may be going on within an isolated system—between, say, kinetic energy and a potential energy or between kinetic energy and thermal energy. However, the total of all the types of energy in the system cannot change.
We can use the rock climber in Fig. 8-15 as an example, approximating her, her gear, and Earth as an isolated system. As she rappels down the rock face, changing the configuration of the system, she needs to control the transfer of energy from the gravitational potential energy of the system. (That energy cannot just disappear.) Some of it is transferred to her kinetic energy. However, she obviously does not want very much transferred to that type or she will be moving too quickly, so she has wrapped the rope around metal rings to produce friction between the rope and the rings as she moves down. The sliding of the rings on the rope then transfers the gravitational potential energy of the system to thermal energy of the rings and rope in a way that she can control. The total energy of the climber–gear–Earth system (the total of its gravitational potential energy, kinetic energy, and thermal energy) does not change during her descent.
For an isolated system, the law of conservation of energy can be written in two ways. First, by setting W = 0 in Eq. 8-35, we get
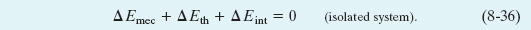
We can also let ΔEmec = Emec,2 − Emec,1, where the subscripts 1 and 2 refer to two different instants—say, before and after a certain process has occurred. Then Eq. 8-36 becomes
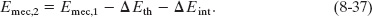
Equation 8-37 tells us:
![]() In an isolated system, we can relate the total energy at one instant to the total energy at another instant without considering the energies at intermediate times.
In an isolated system, we can relate the total energy at one instant to the total energy at another instant without considering the energies at intermediate times.
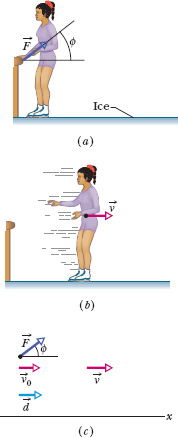
Fig. 8-16 (a) As a skater pushes herself away from a railing, the force on her from the railing is ![]() . (b) After the skater leaves the railing, she has velocity
. (b) After the skater leaves the railing, she has velocity ![]() . (c) External force
. (c) External force ![]() acts on the skater, at angle
acts on the skater, at angle ![]() with a horizontal x axis. When the skater goes through displacement
with a horizontal x axis. When the skater goes through displacement ![]() , her velocity is changed from
, her velocity is changed from ![]() (= 0) to
(= 0) to ![]() by the horizontal component of
by the horizontal component of ![]() .
.
This fact can be a very powerful tool in solving problems about isolated systems when you need to relate energies of a system before and after a certain process occurs in the system.
In Section 8-5, we discussed a special situation for isolated systems—namely, the situation in which nonconservative forces (such as a kinetic frictional force) do not act within them. In that special situation, ΔEth and ΔEint are both zero, and so Eq. 8-37 reduces to Eq. 8-18. In other words, the mechanical energy of an isolated system is conserved when nonconservative forces do not act in it.
External Forces and Internal Energy Transfers
An external force can change the kinetic energy or potential energy of an object without doing work on the object—that is, without transferring energy to the object. Instead, the force is responsible for transfers of energy from one type to another inside the object.
Figure 8-16 shows an example. An initially stationary ice skater pushes away from a railing and then slides over the ice (Figs. 8-16a and b). Her kinetic energy increases because of an external force ![]() on her from the rail. However, that force does not transfer energy from the rail to her. Thus, the force does no work on her. Rather, her kinetic energy increases as a result of internal transfers from the biochemical energy in her muscles.
on her from the rail. However, that force does not transfer energy from the rail to her. Thus, the force does no work on her. Rather, her kinetic energy increases as a result of internal transfers from the biochemical energy in her muscles.
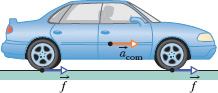
Fig. 8-17 A vehicle accelerates to the right using four-wheel drive. The road exerts four frictional forces (two of them shown) on the bottom surfaces of the tires. Taken together, these four forces make up the net external force ![]() acting on the car.
acting on the car.
Figure 8-17 shows another example. An engine increases the speed of a car with four-wheel drive (all four wheels are made to turn by the engine). During the acceleration, the engine causes the tires to push backward on the road surface. This push produces frictional forces ![]() that act on each tire in the forward direction. The net external force
that act on each tire in the forward direction. The net external force ![]() from the road, which is the sum of these frictional forces, accelerates the car, increasing its kinetic energy. However,
from the road, which is the sum of these frictional forces, accelerates the car, increasing its kinetic energy. However, ![]() does not transfer energy from the road to the car and so does no work on the car. Rather, the car’s kinetic energy increases as a result of internal transfers from the energy stored in the fuel.
does not transfer energy from the road to the car and so does no work on the car. Rather, the car’s kinetic energy increases as a result of internal transfers from the energy stored in the fuel.
In situations like these two, we can sometimes relate the external force ![]() on an object to the change in the object’s mechanical energy if we can simplify the situation. Consider the ice skater example. During her push through distance d in Fig. 8-16c, we can simplify by assuming that the acceleration is constant, her speed changing from v0 = 0 to v. (That is, we assume
on an object to the change in the object’s mechanical energy if we can simplify the situation. Consider the ice skater example. During her push through distance d in Fig. 8-16c, we can simplify by assuming that the acceleration is constant, her speed changing from v0 = 0 to v. (That is, we assume ![]() has constant magnitude F and angle
has constant magnitude F and angle ![]() .) After the push, we can simplify the skater as being a particle and neglect the fact that the exertions of her muscles have increased the thermal energy in her muscles and changed other physiological features. Then we can apply Eq. 7-5
.) After the push, we can simplify the skater as being a particle and neglect the fact that the exertions of her muscles have increased the thermal energy in her muscles and changed other physiological features. Then we can apply Eq. 7-5 ![]() to write
to write
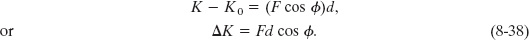
If the situation also involves a change in the elevation of an object, we can include the change ΔU in gravitational potential energy by writing

The force on the right side of this equation does no work on the object but is still responsible for the changes in energy shown on the left side.
Power
Now that you have seen how energy can be transferred from one type to another, we can expand the definition of power given in Section 7-9. There power is defined as the rate at which work is done by a force. In a more general sense, power P is the rate at which energy is transferred by a force from one type to another. If an amount of energy ΔE is transferred in an amount of time Δt, the average power due to the force is

Similarly, the instantaneous power due to the force is
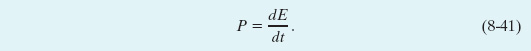
In Fig. 8-18, a 2.0 kg package of tamale slides along a floor with speed v1 = 4.0 m/s. It then runs into and compresses a spring, until the package momentarily stops. Its path to the initially relaxed spring is frictionless, but as it compresses the spring, a kinetic frictional force from the floor, of magnitude 15 N, acts on the package. If k = 10 000 N/m, by what distance d is the spring compressed when the package stops?
Solution: A starting Key Idea is to examine all the forces and then to determine whether we have an isolated system or a system on which an external force is doing work.
Forces: The normal force on the package from the floor does no work on the package because the direction of this force is always perpendicular to the direction of the package’s displacement. For the same reason, the gravitational force on the package does no work. As the spring is compressed, however, a spring force does work on the package, transferring energy to elastic potential energy of the spring. The spring force also pushes against a rigid wall. Because there is friction between the package and the floor, the sliding of the package across the floor increases their thermal energies.
System: The package–spring–floor–wall system includes all these forces and energy transfers in one isolated system. Therefore, a second Key Idea is that, because the system is isolated, its total energy cannot change. We can then apply the law of conservation of energy in the form of Eq. 8-37 to the system:
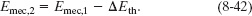
Let subscript 1 correspond to the initial state of the sliding package and subscript 2 correspond to the state in which the package is momentarily stopped and the spring is compressed by distance d. For both states the mechanical energy of the system is the sum of the package’s kinetic energy ![]() and the spring’s potential energy
and the spring’s potential energy ![]() . For state 1, U = 0 (because the spring is not compressed), and the package’s speed is v1. Thus, we have
. For state 1, U = 0 (because the spring is not compressed), and the package’s speed is v1. Thus, we have
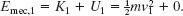
For state 2, K = 0 (because the package is stopped), and the compression distance is d. Therefore, we have
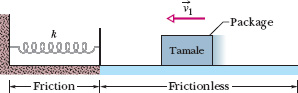
Fig. 8-18 A package slides across a frictionless floor with velocity ![]() toward a spring of spring constant k. When the package reaches the spring, a frictional force from the floor acts on the package.
toward a spring of spring constant k. When the package reaches the spring, a frictional force from the floor acts on the package.
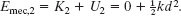
Finally, by Eq. 8-31, we can substitute fkd for the change ΔEth in the thermal energy of the package and the floor. We can now rewrite Eq. 8-42 as
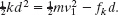
Rearranging and substituting known data give us
5000d2 + 15d − 16 = 0.
Solving this quadratic equation yields
d = 0.055 m = 5.5 cm. (Answer)
In Fig. 8-19, a circus beagle of mass m = 6.0 kg runs onto the left end of a curved ramp with speed v0 = 7.8 m/s at height y0 = 8.5 m above the floor. It then slides to the right and comes to a momentary stop when it reaches a height y = 11.1 m above the floor. The ramp is not frictionless. What is the increase ΔEth in the thermal energy of the beagle and ramp because of the sliding?
Solution: A Key Idea to get us started is to examine all the forces on the beagle and then see whether we have an isolated system or a system on which an external force is doing work.
Forces: The normal force on the beagle from the ramp does no work because its direction is always perpendicular to the direction of the beagle’s displacement. The gravitational force on the beagle does do work as the beagle’s elevation changes. Because of friction between beagle and ramp, the sliding increases their thermal energy.
System: The beagle–ramp–Earth system includes all these forces and energy transfers in one isolated system. Then a second Key Idea is that, because the system is isolated, its total energy cannot change. We can apply the law of conservation of energy in the form of Eq. 8-36 to this system:
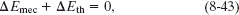
where the energy changes occur between the initial state and the state when the beagle stops momentarily. Also, the change ΔEmec is the sum of the change ΔK in the kinetic energy of the beagle and the change ΔU in the gravitational potential energy of the system, where
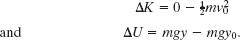
Fig. 8-19 A beagle slides along a curved ramp, starting with speed v0 at height y0 and reaching height y, at which it momentarily stops.
Substituting these expressions into Eq. 8-43 and solving for ΔEth yield
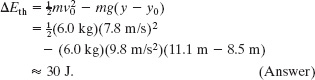
Leave a Reply