We next consider a special case of two-dimensional motion: A particle moves in a vertical plane with some initial velocity 
0 but its acceleration is always the free-fall acceleration 
, which is downward. Such a particle is called a projectile (meaning that it is projected or launched), and its motion is called projectile motion. A projectile might be a tennis ball (Fig. 4-9) or baseball in flight, but it is not an airplane or a duck in flight. Our goal here is to analyze projectile motion using the tools for two-dimensional motion described in Sections 4-2 through 4-4 and making the assumption that air has no effect on the projectile.
Figure 4-10, which is analyzed in the next section, shows the path followed by a projectile when the air has no effect. The projectile is launched with an initial velocity 0 that can be written as
The components v0x and v0y can then be found if we know the angle θ0 between 0 and the positive x direction:
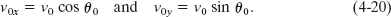
During its two-dimensional motion, the projectile’s position vector 
and velocity vector change continuously, but its acceleration vector 
is constant and always directed vertically downward. The projectile has no horizontal acceleration.
Projectile motion, like that in Figs. 4-9 and 4-10, looks complicated, but we have the following simplifying feature (known from experiment):
Fig. 4-9 A stroboscopic photograph of a yellow tennis ball bouncing off a hard surface. Between impacts, the ball has projectile motion.
In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other.
This feature allows us to break up a problem involving two-dimensional motion into two separate and easier one-dimensional problems, one for the horizontal motion (with zero acceleration) and one for the vertical motion (with constant downward acceleration). Here are two experiments that show that the horizontal motion and the vertical motion are independent.
Two Golf Balls
Figure 4-11 is a stroboscopic photograph of two golf balls, one simply released and the other shot horizontally by a spring. The golf balls have the same vertical motion, both falling through the same vertical distance in the same interval of time. The fact that one ball is moving horizontally while it is falling has no effect on its vertical motion; that is, the horizontal and vertical motions are independent of each other.
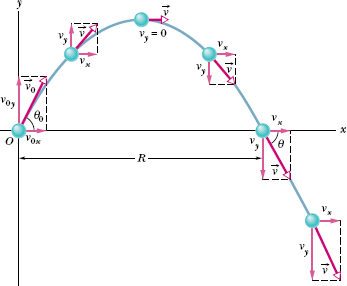
Fig. 4-10 The path of a projectile that is launched at x0 = 0 and y0 = 0, with an initial velocity 
. The initial velocity and the velocities at various points along its path are shown, along with their components. Note that the horizontal velocity component remains constant but the vertical velocity component changes continuously. The range R is the horizontal distance the projectile has traveled when it returns to its launch height.
Fig. 4-11 One ball is released from rest at the same instant that another ball is shot horizontally to the right. Their vertical motions are identical.
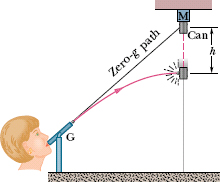
Fig. 4-12 The projectile ball always hits the falling can. Each falls a distance h from where it would be were there no free-fall acceleration.
A Great Student Rouser
Figure 4-12 shows a demonstration that has enlivened many a physics lecture. It involves a blow gun G, using a ball as a projectile. The target is a can suspended from a magnet M, and the tube of the blow gun is aimed directly at the can. The experiment is arranged so that the magnet releases the can just as the ball leaves the blow gun.
If g (the magnitude of the free-fall acceleration) were zero, the ball would follow the straight-line path shown in Fig. 4-12 and the can would float in place after the magnet released it. The ball would certainly hit the can.
However, g is not zero, but the ball still hits the can! As Fig. 4-12 shows, during the time of flight of the ball, both ball and can fall the same distance h from their zero-g locations. The harder the demonstrator blows, the greater is the ball’s initial speed, the shorter the flight time, and the smaller the value of h.
Leave a Reply