Average Acceleration and Instantaneous Acceleration

When a particle’s velocity changes from ₁ to ₂ in a time interval Δt, its average acceleration  during Δt is

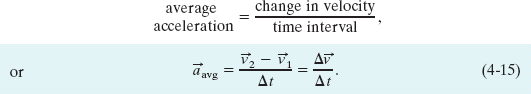
If we shrink Δt to zero about some instant, then in the limit  approaches the instantaneous acceleration (or acceleration)  at that instant; that is,

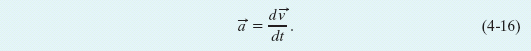
If the velocity changes in either magnitude or direction (or both), the particle must have an acceleration.

We can write Eq. 4-16 in unit-vector form by substituting Eq. 4-11 for  to obtain

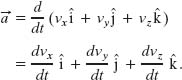
We can rewrite this as

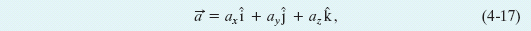
where the scalar components of  are

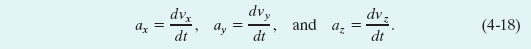
Thus, we can find the scalar components of  by differentiating the scalar components of .

Figure 4-7 shows an acceleration vector  and its scalar components for a particle moving in two dimensions. Caution: When an acceleration vector is drawn, as in Fig. 4-7, it does not extend from one position to another. Rather, it shows the direction of acceleration for a particle located at its tail, and its length (representing the acceleration magnitude) can be drawn to any scale.

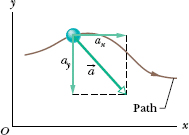
Fig. 4-7   The acceleration  of a particle and the scalar components of .

Sample Problem 4-4

For the rabbit in Sample Problems 4-2 and 4-3, find the acceleration  at time t = 15 s, in unit-vector notation and in magnitude-angle notation.

Solution: There are two Key Ideas here: (1) We can find the rabbit’s acceleration  by first finding the acceleration components. (2) We can find those components by taking derivatives of the rabbit’s velocity components. Applying the a_x part of Eq. 4-18 to Eq. 4-13, we find the x component of  to be

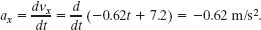
Similarly, applying the a_y part of Eq. 4-18 to Eq. 4-14 yields the y component as

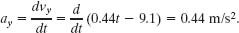
We see that the acceleration does not vary with time (it is a constant) because the time variable t does not appear in the expression for either acceleration component. Equation 4-17 then yields

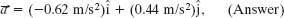
which is shown superimposed on the rabbit’s path in Fig. 4-8.

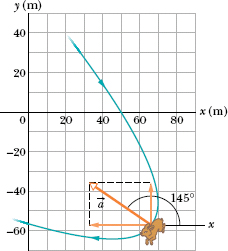
Fig. 4-8   The acceleration  of the rabbit at t = 15 s. The rabbit happens to have this same acceleration at all points on its path.

To get the magnitude and angle of , either we use a vector-capable calculator or we follow Eq. 3-6. For the magnitude we have

For the angle we have

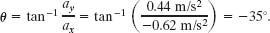
However, this angle, which is the one displayed on a calculator, indicates that  is directed to the right and downward in Fig. 4-8. Yet, we know from the components that  must be directed to the left and upward. To find the other angle that has the same tangent as −35° but is not displayed on a calculator, we add 180°:

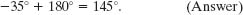
This is consistent with the components of . Note that  has the same magnitude and direction throughout the rabbit’s run because, as we noted previously, the acceleration is constant.

CHECKPOINT 3 Here are four descriptions of the position (in meters) of a puck as it moves in an xy plane:

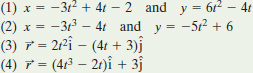
For each description, determine whether the x and y components of the puck’s acceleration are constant and whether the acceleration  is constant.

Sample Problem 4-5

A particle with velocity  (in meters per second) at t = 0 undergoes a constant acceleration  of magnitude a = 3.0 m/s² at an angle θ = 130° from the positive direction of the x axis. What is the particle’s velocity  at t = 5.0 s, in unit-vector notation and in magnitude-angle notation?

Solution: We first note that this is two-dimensional motion, in the xy plane. Then there are two Key Ideas here. First, because the acceleration is constant, Eq. 2-11 (v = v₀ + at) applies. Second, because Eq. 2-11 applies only to straight-line motion, we must apply it separately for motion parallel to the x axis and motion parallel to the y axis; that is, we must find the velocity components v_x and v_y from the equations

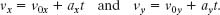
In these equations, v_0x (= −2.0 m/s) and v_0y (= 4.0 m/s) are the x and y components of , and a_x and a_y are the x and y components of . To find a_x and a_y, we resolve  either with a vector-capable calculator or with Eq. 3-5:

a_x = a cos θ = (3.0 m/s²)(cos 130°) = −1.93 m/s²,

a_y = a sin θ = (3.0 m/s²)(sin 130°) = +2.30 m/s².

When these values are inserted into the equations for v_x and v_y, we find that, at time t = 5.0 s,

v_x = −2.0 m/s + (−1.93 m/s²)(5.0 s) = −11.65 m/s,

v_y = 4.0 m/s + (2.30 m/s²)(5.0 s) = 15.50 m/s.

Thus, at t = 5.0 s, we have, after rounding to the correct number of significant figures,

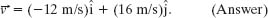
Either using a vector-capable calculator or following Eq. 3-6, we find that the magnitude and angle of  are

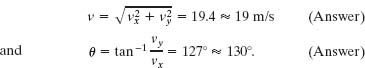
Check the last line with your calculator. Does 127° appear on the display, or does −53° appear? Now sketch the vector  with its components to see which angle is reasonable.

CHECKPOINT 4 If the position of a hobo’s marble is given by , with  in meters and t in seconds, what must be the units of the coefficients 4, −2, and 3?