Vectors and the Laws of Physics

So far, in every figure that includes a coordinate system, the x and y axes are parallel to the edges of the book page. Thus, when a vector  is included, its components a_x and a_y are also parallel to the edges (as in Fig. 3-18a). The only reason for that orientation of the axes is that it looks “proper”; there is no deeper reason. We could, instead, rotate the axes (but not the vector ) through an angle  as in Fig. 3-18b, in which case the components would have new values, call them a_x′ and a_y′. Since there are an infinite number of choices of , there are an infinite number of different pairs of components for .

Which then is the “right” pair of components? The answer is that they are all equally valid because each pair (with its axes) just gives us a different way of describing the same vector ; all produce the same magnitude and direction for the vector. In Fig. 3-18 we have

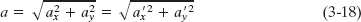
and

The point is that we have great freedom in choosing a coordinate system, because the relations among vectors (including, for example, the vector addition of Eq. 3-1) do not depend on the location of the origin of the coordinate system or on the orientation of the axes. This is also true of the relations of physics; they are all independent of the choice of coordinate system. Add to that the simplicity and richness of the language of vectors and you can see why the laws of physics are almost always presented in that language: one equation, like Eq. 3-10, can represent three (or even more) relations, like Eqs. 3-11, 3-12, and 3-13.

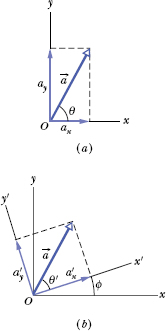
Fig. 3-18 (a) The vector  and its components. (b) The same vector, with the axes of the coordinate system rotated through an angle .