In 1792, the newborn Republic of France established a new system of weights and measures. Its cornerstone was the meter, defined to be one ten-millionth of the distance from the north pole to the equator. Later, for practical reasons, this Earth standard was abandoned and the meter came to be defined as the distance between two fine lines engraved near the ends of a platinum–iridium bar, the standard meter bar, which was kept at the International Bureau of Weights and Measures near Paris. Accurate copies of the bar were sent to standardizing laboratories throughout the world. These secondary standards were used to produce other, still more accessible standards, so that ultimately every measuring device derived its authority from the standard meter bar through a complicated chain of comparisons.
Eventually, modern science and technology required a standard more precise than the distance between two fine scratches on a metal bar. In 1960, a new standard for the meter, based on the wavelength of light, was adopted. Specifically, the standard for the meter was redefined to be 1 650 763.73 wavelengths of a particular orange-red light emitted by atoms of krypton-86 (a particular isotope, or type, of krypton) in a gas discharge tube. This awkward number of wavelengths was chosen so that the new standard would be close to the old meter-bar standard.
By 1983, however, the demand for higher precision had reached such a point that even the krypton-86 standard could not meet it, and in that year a bold step was taken. The meter was redefined as the distance traveled by light in a specified time interval. In the words of the 17th General Conference on Weights and Measures:
The meter is the length of the path traveled by light in a vacuum during a time interval of 1/299 792 458 of a second.
This time interval was chosen so that the speed of light c is exactly
c = 299 792 458 m/s.
Measurements of the speed of light had become extremely precise, so it made sense to adopt the speed of light as a defined quantity and to use it to redefine the meter.
Table 1-3 shows a wide range of lengths, from that of the universe (top line) to those of some very small objects.
PROBLEM-SOLVING TACTICS
TACTIC 2: Order of Magnitude
The order of magnitude of a number is the power of ten when the number is expressed in scientific notation. For example, if A = 2.3 × 104 and B = 7.8 × 104, then the orders of magnitude of both A and B are 4.
Often, engineering and science professionals will estimate the result of a calculation to the nearest order of magnitude. For our example, the nearest order of magnitude is 4 for A and 5 for B. Such estimation is common when detailed or precise data required in the calculation are not known or easily found. Sample Problem 1-3 gives an example.
The world’s largest ball of string is about 2 m in radius. To the nearest order of magnitude, what is the total length L of the string in the ball?
Solution: We could, of course, take the ball apart and measure the total length L, but that would take great effort and make the ball’s builder most unhappy. A Key Idea here is that, because we want only the nearest order of magnitude, we can estimate any quantities required in the calculation.
Let us assume the ball is spherical with radius R = 2 m. The string in the ball is not closely packed (there are uncountable gaps between adjacent sections of string). To allow for these gaps, let us somewhat overestimate the cross-sectional area of the string by assuming the cross section is square, with an edge length d = 4 mm. Then, with a cross-sectional area of d2 and a length L, the string occupies a total volume of
V = (cross-sectional area)(length) = d2L.
This is approximately equal to the volume of the ball, given by 
, which is about 4R3 because π is about 3. Thus, we have
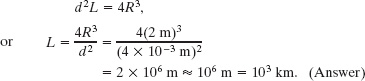
(Note that you do not need a calculator for such a simplified calculation.) To the nearest order of magnitude, the ball contains about 1000 km of string!
Leave a Reply