Now that we have a way of determining the equilibrium potential, let’s look at how we can use it. First, the convention we have adopted tells us that when the circuit is closed, a spontaneous reaction will occur. More specifically, a cathodic or reduction reaction takes place on the positive electrode, and an anodic or oxidation reaction occurs on the negative electrode. Electrochemical cells in which the reactions take place spontaneously to produce electrical current are called galvanic cells. A battery that is discharging is an example of such a cell. The maximum work that can be extracted from such a cell is equal to nFU (see Equation 2.3). However, to achieve this maximum, the cell would need to be discharged at an infinitely slow rate to avoid irreversible losses associated with the generation and movement of current in the cell. We will learn more about current and irreversible losses later in this book. In practice, as a consequence of irreversible processes, the operating voltage of a galvanic cell during discharge is less than the equilibrium voltage. But, as you can see, the equilibrium or thermodynamic potential serves as an essential reference point for the analysis of electrochemical cells.

In contrast to galvanic cells, an electrochemical cell in which energy must be added in order to drive the reactions in the desired direction is called an electrolytic cell. The magnitude of the applied potential, which is the operating voltage of the cell, must be greater than the equilibrium potential since energy must be added to overcome the equilibrium voltage in order to generate and move current through the cell. The chlor-alkali cell in Illustration 2.4 is an example of an electrolytic cell, where the full-cell reaction corresponding to the positive cell potential was opposite the desired direction. Thus, a potential greater than 2.164 V would need to be applied to such a cell in order to produce the desired products.

ILLUSTRATION 2.6

A commonly used battery is the lead–acid battery that you have in your car. The reactions for this battery are as follows:

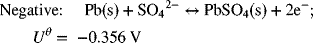
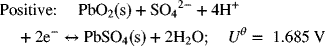
The electrolyte in the battery is about 5 M sulfuric acid. What is the thermodynamic potential of the battery at 25 °C?

The standard cell potential is 1.685 V – (−0.356 V) = 2.041 V.

The complete cell reaction is .

The equilibrium potential (assuming full dissociation of the acid and ion activities equal to the concentration ratios) is

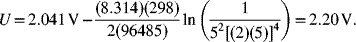
You may be wondering how your car has a 12 V battery and we calculated a cell voltage of just over 2 V. Your car battery contains six battery cells in series. Finally, full dissociation and unit activity coefficients are not good assumptions for the concentrated acid in these batteries, and the actual open-circuit voltage is about 2.13 V at room temperature.

2.8 Equilibrium Constants

The equilibrium constant for a chemical reaction is defined as

(2.26)

Making use of Equation 2.11, the equilibrium constant can be related to the standard potential for the cell,

(2.27)

Also, since U for a reaction at equilibrium is equal to zero (as is ),

(2.28a)

and

(2.28b)

You are probably familiar with the solubility product for a solute dissolving in water. Now we want to see how to use standard cell potential data to calculate it. To do this, let’s determine the solubility product for AgCl. The relevant reaction is the following equilibrium reaction:

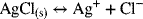
This reaction can be viewed as the sum of the following two half-cell reactions:

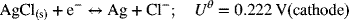
and

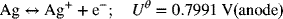
Therefore, at 25 °C,  . From Equations 2.23 and 2.28b,

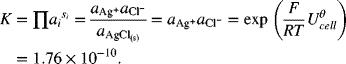
Thus, the equilibrium constant can be readily calculated for any reaction that can be written as the sum of two or more known half-cell reactions. Note that  must be known at the temperature of interest.

The ratio of activities and hence concentrations (if the activity coefficients are known) can also be determined for a half-cell at equilibrium if the cell potential at open circuit, U, is known and the other electrode reaction is fully specified. In this case, the full cell is not at equilibrium.