Another important quantity in the study of electrochemical systems is the potential. We can define an electrostatic potential, ϕ, in terms of the work required to move a unit (positive) charge from infinity to a specific position in the metal or in solution. This work can also be thought of in terms of energy. The unit for potential is a volt [V], which is also [J·C−1]. Since we are frequently interested in the potential of the electrodes, and since these are generally metals where electrons are the carriers of current, we can think of potential as a measure of the energy of the electron in the metal. Thus, the cell potential measured with a voltmeter in Figure 1.1 represents the difference in electron energy in the two electrodes.
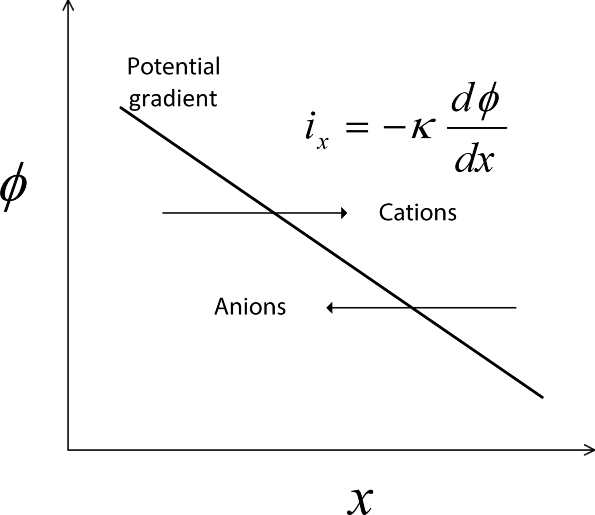
As you may have guessed, the flow of current in metals and in electrolyte solutions is critical to the understanding and analysis of electrochemical systems. A potential difference in a metal or in an electrolyte leads to the flow of current. The difference is often expressed in terms of a potential gradient, which is the rate of change in potential with distance. By convention, electric current is defined as flowing from high potential to low potential, which is the direction that a positive charge would move due to the difference in the potential. This situation is illustrated in Figure 1.3. Current in a metal (e.g., wire) is due to electron flow. Since electrons are negatively charged, electrons travel from low potential to high potential. Ohm’s law relates the current and potential. For one-dimensional conduction (current flow),
where κ is the electrical conductivity of the electrolyte. The electrical conductivity is a property that characterizes how well the material moves electrical charge; it has units of [S·m−1]. If the current density is constant, Equation 1.15 can be integrated to give
This equation applies to one-dimensional current flow in an electrolyte of constant composition. A similar expression also applies to metals in general.
ILLUSTRATION 1.7
A fuel cell used for an automotive application operates at a current of 350 A. If the electrode area of each cell is 0.04 m2, what is the current density? If the distance between the electrodes is 0.07 mm, and the conductivity of the electrolyte is 10 S·m−1, what is the potential drop (difference in volts) across the electrolyte?
The current density, i, is simply the current divided by the electrode area
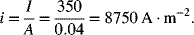
Ohm’s law is used to calculate the drop in potential across the electrolyte:
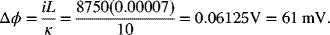
Compare these results with the potential drop in 10 cm long copper wire with a diameter of 1 cm. The conductivity of copper is much higher: 5.85 × 107 S·m−1. The same current flows through the wire, but the cross-sectional area (Aw = 7.9 × 10−5 m−2) is smaller
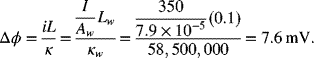
Leave a Reply