15.1. Using Fig. 15.5 on page 602, without performing additional calculations, sketch the P-x-y diagram at 400 K showing the two-phase region. Make the sketch semi-quantitative to show the values where the phase envelope touches the axes of your diagram. Label the bubble and dew lines. Also indicate the approximate value of the maximum pressure.
15.2. Consider two gases that follow the virial equation. Show that an ideal mixture of the two gases follows the relation B = y1B11 + y2B22.
15.3. Consider phase equilibria modeled with 
. When might ϕi be replaced by ϕi for each phase? When might ϕi = 1 be used for each phase? Discuss the appropriateness of using the virial equation for mixtures to solve phase behavior using the expression .
15.4. Calculate the molar volume of a binary mixture containing 30 mol% nitrogen(1) and 70 mol% n-butane(2) at 188°C and 6.9 MPa by the following methods.
a. Assume the mixture to be an ideal gas.
b. Assume the mixture to be an ideal solution with the volumes of the pure gases given by
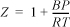
and the virial coefficients given below.
c. Use second virial coefficients predicted by the generalized correlation for B.
d. Use the following values for the second virial coefficients.
Data:
B11 = 14 B22 = –265 B12 = –9.5 (Units are cm3/gmole)
e. Use the Peng-Robinson equation.
15.5. For the same mixture and experimental conditions as problem 15.4, calculate the fugacity of each component in the mixture, 
. Use methods (a) – (e).
15.6. A vapor mixture of CO2 (1) and i-butane (2) exists at 120°C and 2.5 MPa. Calculate the fugacity of CO2 in this mixture across the composition range using
a. The virial equation for mixtures
b. The Peng-Robinson equation
c. The virial equation for the pure components and an ideal mixture model.
15.7. Use the virial equation to consider a mixture of propane and n-butane at 515 K at pressures between 0.1 and 4.5 MPa. Verify that the virial coefficient method is valid by using Eqn. 7.10.
a. Prepare a plot of fugacity coefficient for each component as a function of composition at pressures of 0.1 MPa, 2 MPa, and 4.5 MPa.
b. How would the fugacity coefficient for each component depend on composition if the mixture were assumed to be ideal, and what value(s) would it have for each of the pressures in part (a)? How valid might the ideal-solution model be for each of these conditions?
c. The excess volume is defined as 
, where V is the molar volume of the mixture, and Vi is the pure component molar volume at the same T and P. Plot the prediction of excess volume of the mixture at each of the pressures from part (a). How does the excess volume depend on pressure?
d. Under which of the pressures in part (a) might the ideal gas law be valid?
15.8. Consider a mixture of nitrogen(1) + n-butane(2) for each of the options: (i) 395 K and 2 MPa; (ii) 460 K and 3.4 MPa; (iii) 360 K and 1 MPa.
a. Calculate the fugacity coefficients for each of the components in the mixture using the virial coefficient correlation. Make a table for your results at y1 = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0. Plot the results on a graph. On the same graph, plot the curves that would be used for the mixture fugacity coefficients if an ideal mixture model were assumed. Label the curves.
b. Calculate the fugacity of each component in the mixture as predicted by the virial equation, an ideal-mixture model, and the ideal-gas model. Prepare a table for each component, and list the three predicted fugacities in three columns for easy comparison. Calculate the values at y1 = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0.
15.9. The virial equation Z = 1 + BP/RT may be used to calculate fugacities of components in mixtures. Suppose B = y1B11 + y2B22. (This simple form makes calculations easier. Eqn. 15.1 gives the correct form.) Use this simplified expression and the correct form to calculate the respective fugacity coefficient formulas for component 1 in a binary mixture.
15.10. The Lewis-Randall rule is usually valid for components of high concentration in gas mixtures. Consider a mixture of 90% ethane and 10% propane at 125°C and 170 bar. Estimate for ethane.
15.11. One of the easiest ways to begin to explore fugacities in nonideal solutions is to model solubilities of crystalline solids dissolved in high pressure gases. In this case, the crystalline solids remain as a pure phase in equilibrium with a vapor mixture, and the fugacity of the “solid” component must be the same in the crystalline phase as in the vapor phase. Consider biphenyl dissolved in carbon dioxide, using kij = 0.100. The molar volume of crystalline biphenyl is 156 cm3/mol.
a. Calculate the fugacity (in MPa) of pure crystalline biphenyl at 310 K and 330 K and 0.1, 1, 10, 15, and 20 MPa.
b. Calculate and plot the biphenyl solubility for the isotherm over the pressure range. Compare the solubility to the ideal gas solubility of biphenyl where the Poynting correction is included, but the gas phase nonidealities are ignored.
15.12. Repeat problem 15.11, except consider naphthalene dissolved in carbon dioxide, using kij = 0.109. The molar volume of crystalline naphthalene is 123 cm3/mol.
15.13. A vessel initially containing propane at 30°C is connected to a nitrogen cylinder, and the pressure is isothermally increased to 2.07 MPa. What is the mole fraction of propane in the vapor phase? You may assume that the solubility of N2 in propane is small enough that the liquid phase may be considered pure propane. Calculate using the following data at 30°C.
15.14. A 50-mol% mixture of propane(1) + n-butane(2) enters a flash drum at 37°C. If the flash drum is maintained at 0.6 MPa, what fraction of the feed exits as a liquid? What are the compositions of the phases exiting the flash drum? Work the problem the following two ways.
a. Use Raoult’s law.
b. Assume ideal mixtures of vapor and liquid (Ki is independent of composition).
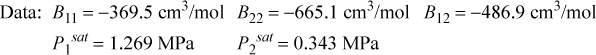
15.15. A mixture containing 5 mol% ethane, 57 mol% propane, and 38 mol% n-butane is to be processed in a natural gas plant. Estimate the bubble-point pressure, the liquid composition, and K-ratios of the coexisting vapor for this mixture at all pressures above 1 bar at which two phases exist. Set kij = 0. Use the shortcut K-ratio method. Plot ln P versus 1/T for your results. What does this plot look like? Plot log Ki versus 1/T. What values do the Ki approach?
15.16. Vapor-liquid equilibria are usually expressed in terms of K factors in petroleum technology. Use the Peng-Robinson equation to estimate the values for methane and benzene in the benzene + methane system with equimolar feed at 300 K and a total pressure of 30 bar and compare to the estimates based on the shortcut K-ratio method.
15.17. Benzene and ethanol form azeotropic mixtures. Prepare a y-x and a P-x-y diagram for the benzene + ethanol system at 45°C assuming the Peng-Robinson model and using the experimental pressure at xE = 0.415 to estimate k12. Compare the results with the experimental data of Brown and Smith cited in problem 10.2.
15.18. A storage tank is known to contain the following mixture at 45°C and 15 bar on a mole basis: 31% ethane, 34% propane, 21% n-butane, 14% i-butane. What is the composition of the coexisting vapor and liquid phases, and what fraction of the molar contents of the tank is liquid?
15.19. The CRC Handbook lists the atmospheric pressure azeotrope for ethanol + methylethylketone at 74.8°C and 34 wt% ethanol. Estimate the value of the Peng-Robinson k12 for this system.
15.20. The CRC Handbook lists the atmospheric pressure azeotrope for methanol + toluene at 63.7°C and 72 wt% methanol. Estimate the value of the Peng-Robinson k12 for this system.
15.21. Use the Peng-Robinson equation for the ethane/heptane system.
a. Calculate the P-x-y diagram at 283 K and 373 K. Use k12 = 0. Plot the results.
b. Based on a comparison of your diagrams with what would be predicted by Raoult’s law at 283 K, does this system have positive or negative deviations from Raoult’s law?
15.22. One mol of n-butane and one mol of n-pentane are charged into a container. The container is heated to 90°C where the pressure reads 7 bar. Determine the quantities and compositions of the phases in the container.
15.23. Consider a mixture of 50 mol% n-pentane and 50 mol% n-butane at 15 bar.
a. What is the dew temperature? What is the composition of the first drop of liquid?
b. At what temperature is the vapor completely condensed if the pressure is maintained at 15 bar? What is the composition of the last drop of vapor?
15.24. LPG gas is a fuel source used in areas without natural gas lines. Assume that LPG may be modeled as a mixture of propane and n-butane. Since the pressure of the LPG tank varies with temperature, there are safety and practical operating conditions that must be met. Suppose the desired maximum pressure is 0.7 MPa, and the lower limit on desired operation is 0.2 MPa. Assume that the maximum summertime tank temperature is 50°C, and that the minimum wintertime temperature is –10°C. [Hint: On a mass basis, the mass of vapor within the tank is negligible relative to the mass of liquid after the tank is filled.]
a. What is the upper limit (mole fraction) of propane for summertime propane content?
b. What is the lowest wintertime pressure for this composition from part (a)?
c. What is the lower limit (mole fraction) of propane for wintertime propane content?
d. What is the highest summertime pressure for this composition from part (b)?
15.25. The kij for the pentane + acetone system has been fitted to a single point in problem P15.6. Generate a P-x-y diagram at 312.75 K.
15.26. The synthesis of methylamine, dimethylamine, and trimethylamine from methanol and ammonia results in a separation train involving excess ammonia and converted amines. Use the Peng-Robinson equation with kij = 0 to predict whether methylamine + dimethylamine, methylamine + trimethylamine, or dimethylamine + trimethylamine would form an azeotrope at 2 bar. Would the azeotropic behavior identified above be altered by raising the pressure to 20 bar? Locate experimental data relating to these systems in the library. How do your predictions compare to the experimental data?
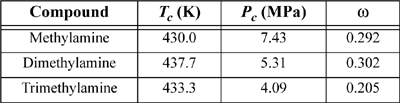
15.27. For the gas/solvent systems below, we refer to the “gas” as the low molecular weight component. Experimental solubilities of light gases in liquid hydrocarbons are tabulated below. The partial pressure of the light gas is 1.013 bar partial pressure. Do the following for each assigned system.
a. Estimate the partial pressure of the liquid hydrocarbon by calculating the pure component vapor pressure via the Peng-Robinson equation, and by subsequently applying Raoult’s law for that component.
b. Estimate the total pressure and vapor composition using the results of step (a).
c. Use the Peng-Robinson equation with kij = 0 to calculate the vapor and liquid compositions that result in 1.013 bar partial pressure of the light gas and compare the pressure and gas phase composition with steps (a) and (b).
d. Henry’s law asserts that 
, when xi is near zero, and hi is the Henry’s law constant. Calculate the Henry’s law constant from the calculations of part (c).
e. Calculate the solubility expected at 2 bar partial pressure of light gas by using Henry’s law as well as by the Peng-Robinson equation and comment on the results.
15.28. Estimate the solubility of carbon dioxide in toluene at 25°C and 1 bar of CO2 partial pressure using the Peng-Robinson equation with a zero binary interaction parameter. The techniques of problem 15.27 may be helpful.
15.29. Oxygen dissolved in liquid solvents may present problems during use of the solvents.
a. Using the Peng-Robinson equation and the techniques introduced in problem 15.27, estimate the solubility of oxygen in n-hexane at an oxygen partial pressure of 0.21 bar.
b. From the above results, estimate the Henry’s law constant.
15.30. Estimate the solubility of ethylene in n-octane at 1 bar partial pressure of ethylene and 25°C. The techniques of problem 15.27 may be helpful. Does the system follow Henry’s law up to an ethylene partial pressure of 3 bar at this temperature? Provide the vapor compositions and total pressures for the above states.
15.31. Henry’s law asserts that , when xi is near zero, and hi is the Henry’s law constant. Gases at high reduced temperatures can exhibit peculiar trends in their Henry’s law constants. Use the Peng-Robinson equation to predict the Henry’s law constant for hydrogen in decalin at T = [300 K, 600 K]. Plot the results as a function of temperature and compare to the prediction from the shortcut prediction. Describe in words the behavior that you observe.
15.32. A gas mixture follows the equation of state
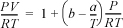
where b is the size parameter, 
, and a is the energetic parameter, 
. Derive the formula for the partial molar enthalpy for component 1 in a binary mixture, where the reference state for both components is the ideal gas state of TR, PR, and the pure component parameters are temperature-independent.
15.33. The procedure for calculation of the residual enthalpy for a pure gas is shown in Example 8.5 on page 316. Now consider the residual enthalpy for a binary gas mixture. For this calculation, it is necessary to determine da/dT for the mixture.
a. Write the form of this derivative for a binary mixture in terms of da1/dT and da2/dT based on the conventional quadratic mixing rule and geometric mean combining rule with a nonzero kij.
b. Provide the expression for the residual enthalpy for a binary mixture that follows the Peng-Robinson equation.
c. A mixture of 50 mol% CO2 and 50 mol% N2 enters a valve at 7 MPa and 40°C. It exits the valve at 0.1013 MPa. Explain how you would determine whether CO2 precipitates, and if so, whether it would be a liquid or solid.
15.34. A gaseous mixture of 30 mol% CO2 and 70 mol% CH4 enters a valve at 70 bar and 40°C and exits at 5.3 bar. Does any CO2 condense? Assume that the mixture follows the virial equation. Assume that any liquid that forms is pure CO2. The vapor pressure of CO2 may be estimated by the shortcut vapor pressure equation. CO2 sublimes at 0.1013 MPa and –78.8°C, although freezing is less likely.
15.35. The vapor-liquid equilibria for the system acetic acid(1) + acetone(2) needs to be characterized in order to simulate an acetic anhydride production process. Experimental data for this system at 760 mmHg have been reported by Othmer (1943)4 as summarized below. Use the data at the equimolar composition to determine a value for the binary interaction parameter of the Peng-Robinson equation. Based on the value you determine for the binary interaction parameter, determine the percent errors in the Peng-Robinson prediction for this system at a mole fraction of x(1) = 0.3.
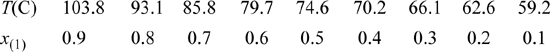
15.36. A mixture of methane and ethylene exists as a single gas phase in a spherical tank (10 m3) on the grounds of a refinery. The mixture is at 298 K and 1 MPa. It is a spring day, and the atmospheric temperature is also 298 K. The mole fraction of ethylene is 20 mol%. Your supervisor wants to draw off gas quickly from the bottom of the tank until the pressure is 0.5 MPa. However, being astute, you suggest that depressurization will cause the temperature to fall, and might cause condensation.
a. Provide a method to calculate the change in temperature with respect to moles removed or tank pressure valid up until condensation starts. Assume the depressurization is adiabatic and reversible. Provide relations to find answers, and ensure that enough equations are provided to calculate numerical values for all variables, but you do not need to calculate a final number.
b. Would the answer in part (a) provide an upper or lower limit to the expected temperature?
c. Outline how you could find the P, T, n of the tank where condensation starts. Provide relations to find answers, and ensure that enough equations are provided to calculate numerical values for all variables, but you do not need to calculate a final number.
a. At 298 K, butane follows the equation of state: P(V – b) = RT at moderate pressures, where b is a function of temperature. Calculate the fugacity for butane at a temperature of 298 K and a pressure of 1 MPa. At this temperature, b = –732 cm3/mol.
b. Pentane follows the same equation of state with b = –1195 cm3/mol at 298 K. In a mixture, b follows the mixing rule: 
where b12 = –928 cm3/mol. Calculate the fugacity of butane in a 20 mol% concentration in pentane at 298 K and 1 MPa, assuming the mixture is an ideal solution.
15.38. The Soave equation of state is:
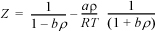
where the mixing and combining rules are given by Eqns. 15.8 and 15.9. Develop an expression for the fugacity coefficient and compare it to the expression given by Soave (1972. Chem. Eng. Sci. 27:1197).
15.39. The following equation of state has been proposed for hard-sphere mixtures:
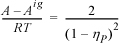
where 
Derive an expression for the fugacity coefficient.
15.40. The equation of state below has been suggested. Derive the expression for the fugacity coefficient.
Z = 1 + 4cρ/(1 – bρ)
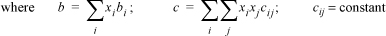
15.41. The following free energy model has been suggested as part of a new equation of state for mixtures. Derive the expression for the fugacity coefficient of component 1.
CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply