Since a compositional derivative is necessary to obtain the partial molar quantities, and the compositions are present in summation terms, we must understand the procedures for differentiation of the sums. Since all of the compositional dependence is embedded in these terms, if we understand how these terms are handled, we can then apply the results to any equation of state. Only three types of sums appear in most forms of equations of state, which have been introduced above. The first type of derivative we will encounter is of the form
![]() Since the compositional dependence is within the mixing rule, if we understand how to differentiate the general mixing rules, then we can easily apply them to the models that use them.
Since the compositional dependence is within the mixing rule, if we understand how to differentiate the general mixing rules, then we can easily apply them to the models that use them.

where ![]() . For a binary nb = n1b1 + n2b2, and k will be encountered once in the sum, whether k = 1 or k = 2, thus:
. For a binary nb = n1b1 + n2b2, and k will be encountered once in the sum, whether k = 1 or k = 2, thus:
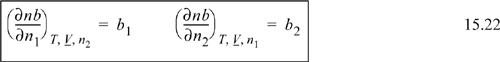
and the general result is

The second type of derivative which we will encounter is of the form

n2a may be written as ![]() . For a binary mixture,
. For a binary mixture, ![]() . Taking the appropriate derivative,
. Taking the appropriate derivative,
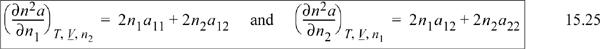
The general result is

For the virial equation, we need to differentiate a function that will look like:
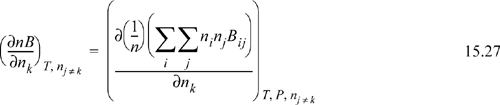
Differentiation by the product rule gives
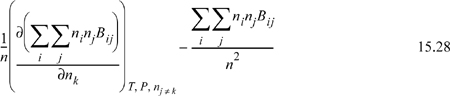
The double sum in the derivative is n2B which we have evaluated in equivalent form in Eqn. 15.25. The second term is just B given by Eqn. 15.1. Therefore, we have for a binary mixture
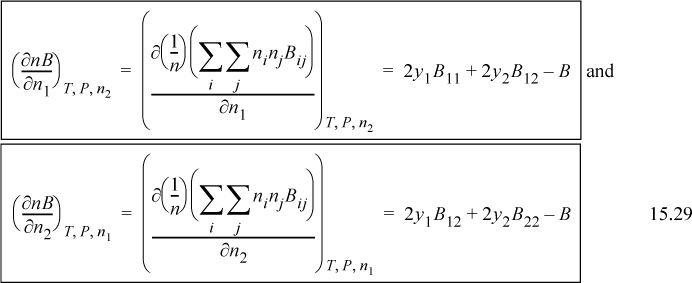
The general result is
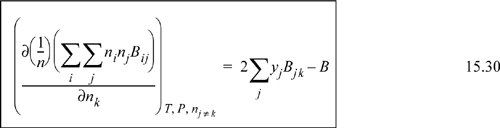
Example 15.3. Fugacity coefficient from the virial equation
For moderate deviations from the ideal-gas law, a common method is to use the virial equation given by:
Z = 1 + BP/RT
where ![]() . Develop an expression for the fugacity coefficient.
. Develop an expression for the fugacity coefficient.
Solution
For the virial equation, we have the result of Eqn. 9.30, ![]()
Applying Eqn. 15.12
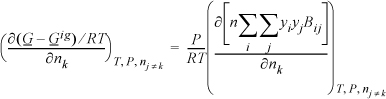
the argument we need to differentiate looks like ![]() .
.
Differentiation has been performed in Eqn. 15.29, which we can generalize as
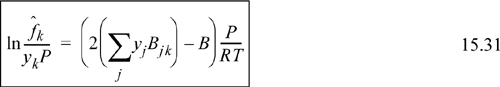
which has been shown earlier for a binary in Eqn. 15.14.
Example 15.4. Fugacity coefficient from the van der Waals equation
Van der Waals’ equation of state provides a simple but fairly accurate representation of key equation of state concepts for mixtures. The main manipulations developed for this equation are the same for other equations of state but the algebra is a little simpler. Recalling van der Waals’ equation from Chapter 6,
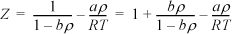
where ![]() and
and ![]() . Develop an expression for the fugacity coefficient.
. Develop an expression for the fugacity coefficient.
Solution
We need to apply Eqn. 15.17. For the departure, we apply Eqn. 8.27 because the differentiation indicated above is performed at constant volume, not constant pressure.
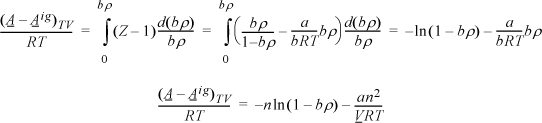
Apply Eqn. 15.17, but instead of differentiating directly, use the chain rule, Eqn. 6.16.
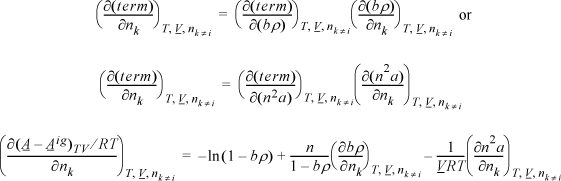
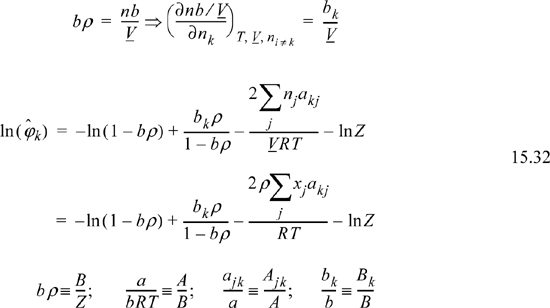
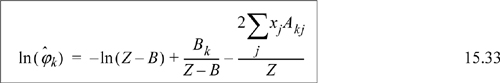
Example 15.5. Fugacity coefficient from the Peng-Robinson equation
The Peng-Robinson equation is given by
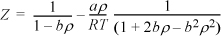
where ![]() and
and ![]() . Develop an expression for the fugacity coefficient.
. Develop an expression for the fugacity coefficient.
Solution
We need to apply Eqn. 15.17. From integration for the pure fluid,
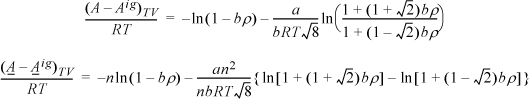
The next steps look intimidating. Basically, they apply the same procedure for differentiation as the last example.

Note a simplification that is not obvious:
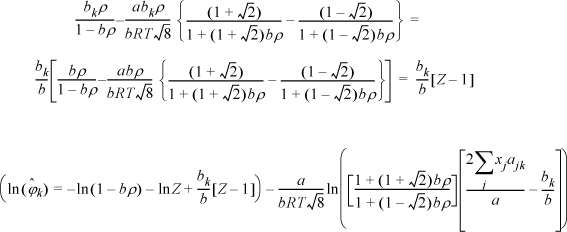
Substituting the following definitions,
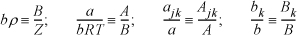
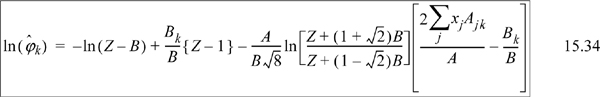
Leave a Reply