Fugacity and Chemical Potential from an EOS

We begin with a reminder that for phase equilibria calculations, that the fugacities of components are needed. The tool that we need for VLE calculations is the K-ratio and an expression for the component fugacity. In Section 10.9 we demonstrated that the component fugacity for an ideal gas component is equal to the partial pressure. In this chapter we develop a method of “correcting” the partial pressure to provide the fugacity. As a variation of the Venn diagram presented in Fig. 11.8, we present the schematic shown in Fig. 15.1. Because the equation of state is capable of representing liquid phases by using the smaller root, we show both vapor and liquid phases.

Figure 15.1. Schematic showing the equation of state approach to modeling fugacities of components. Departure function (fugacity coefficient) methods are used for both the vapor and liquid phases. Superscripts are used to distinguish the fugacity coefficients of each phase. Liquid-phase compositions are conventionally denoted by x_i and vapor-phase compositions by y_i.

The method of deriving the fugacity is an extension of Eqn. 10.39. If we compare the chemical potential in the real mixture to the chemical potential for an ideal gas, we see that the difference is given by the component derivative of the Gibbs departure.

We have seen the Gibbs departure in Eqns. 9.23 and 9.31. For the virial equation, we have

where we recognize that the virial coefficient depends on composition via Eqn. 15.2. By differentiation of this expression, we obtain the chemical potential. We can calculate the component fugacity if we use Eqn. 11.22 and replace the standard state with the ideal gas mixture state. Since the component fugacity in the ideal gas state is the partial pressure, the fugacity coefficient becomes

 General form of fugacity coefficient in a mixture useful for EOSs of the form Z(T,P).

We define the ratio of the component fugacity to the partial pressure (ideal gas component fugacity) as the component fugacity coefficient.

 Component fugacity coefficient.

Differentiation of the Gibbs departure leads to the component fugacity coefficients for a binary,

 Fugacity coefficient for virial equation of state.

which will be shown in more detail later. The fugacity coefficient of a component in a mixture may be directly determined at a given T and P by evaluating the virial coefficients at the temperature, then using this equation to calculate the fugacity coefficient.

Differentiation of the Gibbs departure function is difficult for a pressure-explicit equation of state like the Peng-Robinson equation of state. The difficulty arises because the Gibbs departure function is given in terms of volume and temperature rather than pressure (Eqns. 8.36 and 9.33), and differentiation at constant pressure as required by Eqn. 15.12 is difficult. As in the case of pure fluids, classical thermodynamics provides the means to solve this problem. Instead of differentiating the Gibbs departure function, we differentiate the Helmholtz departure function. Recalling,

and noting,

we also use A = G – PV, or dA = dG – d(PV):

Equating coefficients of dn_i we see an alternative method to find the chemical potential,

Note that T, P, and V identify the same conditions for the real fluid. Therefore, when we evaluate the departure, the ideal gas state must be corrected from V^ig to V,

where the notation (A – A^ig)_TV denotes a departure function at the same T, V, which is the integral of Eqn. 8.27. The last term, ln Z, represents the correction of the ideal gas Helmholtz energy from V to V^ig. Careful inspection of the true form on the integral leading to ln Z should convince you that differentiation does not change this term, and only the integral for the departure in Eqn. 15.16 must be differentiated.

 General form for fugacity coefficient for a pressure explicit equation of state such as the Peng-Robinson, that is, Z(T,ρ).

Therefore, the fugacity coefficient is calculated using

To apply this, consider the Peng-Robinson equation as an example.

By extending the method of reducing the equation of state parameters developed in Eqns. 7.21 and 7.22,  and , where . Then, differentiation as we will show in Example 15.5 on page 592, yields for a binary system

 Fugacity coefficient for the Peng-Robinson equation of state in dimensionless form.

As we saw in the case of equations of state for pure fluids, there is no fundamental reason to distinguish between the vapor and liquid phases except by the magnitude of Z. The equation of state approach encompasses both liquids and vapors very simply. We replace the vapor phase mole fractions with liquid phase mole fractions in all formulas including those for A and B, resulting in

Recalling that  at equilibrium, we write the equality and rearrange to find the expression for the K-ratio used to solve VLE problems.

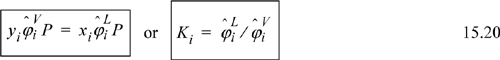
 Eqn. 15.20 provides the primary equations for VLE via equations of state. Different equations of state provide different formulas for .

Given K_i for all i, it is straightforward to solve VLE problems using the same procedures as for ideal solutions.

Note: Eqns. 15.20 provide the primary equations for VLE via equations of state. These equations are implemented by iteration procedures summarized in Appendix C. Only the bubble method will be presented in the chapter in detail. Although cubic equations can represent both vapor and liquid phases, note that the virial equation cannot be used for liquid phases.

Bubble-Pressure Method

For a bubble-pressure calculation, the T and all x_i are known as shown in Table 10.1 on page 373. Like the simple calculation performed in the preceding chapter, the criterion for convergence is  which needs to be expressed in terms of variables for the current method. Rearranging Eqn. 15.20, this sum becomes . Unlike the activity model calculations, we cannot explicitly solve for pressure because all  and  depend on pressure. Additionally,  all depend on composition of the vapor phase, which is not exactly known until the problem is solved. Typically, we use Raoult’s law with the shortcut vapor pressure equation for the first guesses of y_i and P. From these values, we determine all K_i and check the sum of y values. If the sum is greater than one, the pressure guess is increased, if less than one, the pressure guess is decreased. A complete flowchart and example will be discussed in Section 15.4, but for now, let us explore the methods for calculating the fugacity coefficients.

As we observed for pure fluids, it is important to select the proper root when applying an equation of state. Considering the Workbook Prfug.xlsx, for the one-root region, we should select that row for the fugacity coefficients. For the three-root region, we should choose the root with the lowest mixture fugacity. At low pressure and near room temperature, systems are usually in the three-root region for both liquid and vapor compositions, but that may change as we approach the critical region. The number of roots depends on composition as well as T and P. For example, it often occurs that one root occurs using the vapor composition when one component is supercritical in equilibrium with a liquid phase. This means we need to select among at least four possibilities for each phase when computing the K-values: largest Z root for vapor composition, smallest Z root with liquid composition, single root with vapor composition, single root with liquid composition. If we compute K-values with all four ratios, only one of the possibilities provides meaningful results and these are the ones to apply in the next iteration.

 Prfug.xlsx may be helpful in following this example.

---

Example 15.2. K-values from the Peng-Robinson equation

The bubble-point pressure of an equimolar nitrogen (1) + methane (2) system is to be calculated by the Peng-Robinson equation and compared to the shortcut K-ratio estimate at 100 K. The shortcut K-ratio estimate will be used as an initial guess: P = 0.4119 MPa, y_N2 = 0.958. Apply the formulas for the fugacity coefficients to obtain an estimate of the K-values for nitrogen and methane and evaluate the sum of the vapor mole fractions based on this initial guess.

Solution

The spreadsheet Prfug.xlsx may be used to follow the calculations. The K-values using the vapor root with vapor composition and liquid root with liquid composition are valid throughout the iterations of this example. From the shortcut calculation, P = 0.4119 MPa at 100 K. Applying Eqns. 7.21 and 7.22 for the pure component parameters:

For N₂: A₁₁ = 0.09686; B₁ = 0.011906;
For CH₄: A₂₂ = 0.18242; B₂ = 0.013266
By the square-root combining rule Eqn. 15.9: A₁₂ = 0.13293

Based on the vapor composition of the shortcut estimate at y₁ = 0.958, the mixing rule gives A^V = 0.099913; B^V = 0.01196; Solving the cubic for the vapor root at this composition gives Z^V = 0.9059.

Then

Many of the terms are the same for the methane in the mixture:

To save some tedious calculations, the liquid formulas have already been applied to obtain: ; . Determining the K values,

y₁ = 0.5 · 1.955 = 0.978; y₂ = 0.5 · 0.1106 = 0.055; 

A higher guess for P would be appropriate for the next iteration in order to make the K-values smaller.  and  would need to be evaluated at the new pressure. The calculations are obviously tedious. K_i calculations are possible in Excel by first copying the “Fugacities” sheet on Prfug.xlsx, using one sheet for liquid and the other for vapor, and then referencing cells on one of the sheets to calculate the K_i. We provide an example of such an arrangement in Prmix.xlsx. More details on the entire procedure will follow in Section 15.4.