VLLE with Immiscible Components

A special case of VLLE is obtained when one of the liquid-phase components is almost entirely insoluble in other components, and all other components are essentially insoluble in it, as occurs with many hydrocarbons with water. When a mixture forms two liquid phases, the mole fractions sum to unity in each of the phases. When a vapor phase coexists, it is a mixture of all components. The bubble pressure can be calculated using Eqn. 14.2, where the liquid phase fugacities are used to calculate the vapor phase partial pressures. For example, water and n-pentane are extremely immiscible. Applying the strategy used in Example 14.1, each liquid phase is essentially pure, resulting in the bubble pressure  which is greater than the bubble point of either component. Rather than considering the bubble pressure, think about the bubble temperature. Since each component contributes to the partial pressure, the bubble temperature of a mixture of two immiscible liquids is lower than the bubble temperature of either pure component at a specified pressure. This phenomenon can be use to permit boiling at a lower temperature as shown in the next example.

---

Example 14.5. Steam distillation

Consider a steam distillation with the vapor leaving the top of the fractionating column and entering the condenser at 0.1 MPa with the following analysis:

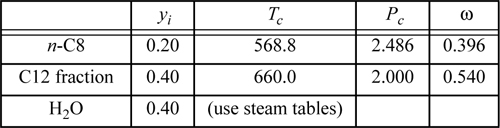
Assuming no pressure drop in the condenser and that the water and hydrocarbons are completely immiscible, calculate the maximum temperature which ensures complete condensation at 0.1 MPa. Use the shortcut K-ratio method for the hydrocarbons.

Solution

Apply the following notation to designate the phases:

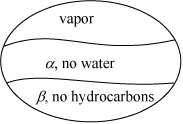
The temperature that we seek is a bubble temperature of the liquid phases. The hydrocarbons and the water are essentially immiscible. We may approximate the hydrocarbon liquid phase, α, as an ideal solution of C8 and C12 with no water present. Therefore, two liquid phases will form: one of pure H₂O and the other a mixture of 1/3 n-C8 + 2/3 C12 fraction. We may apply Raoult’s law with x_w = 1 for water in the β phase. The vapor mixture is a single phase, however, and must conform to: .

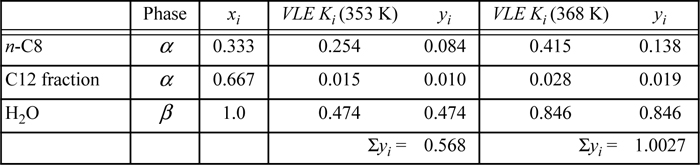
So the bubble temperature with water present is ~95°C. Note that the bubble temperature is below the bubble temperature of pure water. What would it be without water?

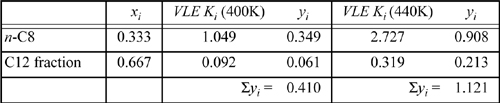
Then, interpolating T ≈ 400 + (1 – 0.41)/(1.121 – 0.41)·40 = 433 K. Thus, we reduced the bubble temperature by 65°C in the steam distillation.