Wilson’s Equation

Wilson² made a bold assumption regarding the temperature dependence of Ω_ij. Wilson’s original parameter used in the literature is Λ_ji, but it is related to Ω_ij in a very direct way. Wilson assumes³

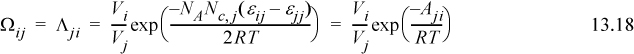
(note: Λ_ii = Λ_jj = 1, and A_ij ≠ A_ji even though ε_ij = ε_ji), and integration with respect to T becomes very simple. Assuming N_c,j = 2 for all j at all ρ,

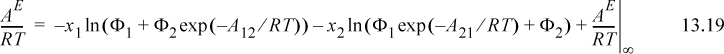
A convenient simplifying assumption before proceeding further is that G^E ~ A^E. This corresponds to neglecting the excess volume of mixing relative to the other contributions and is quite acceptable for liquids. The customary way of interpreting G^E/RT is to separate it into an energetic part known as the residual contribution, (G^E/RT)^RES, that vanishes at infinite temperature or when ε₁₂ – ε₂₂ = 0 and ε₂₁ – ε₁₁ = 0, and a size/shape part known as the combinatorial contribution, (G^E/RT)^COMB, that represents the infinite temperature limit at the liquid density. For Wilson’s equation, the first two terms vanish at high T, so

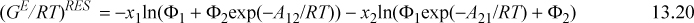
For the combinatorial contribution, Wilson used Flory’s equation,

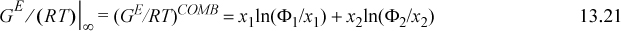
It should be noted that the assumption of the temperature dependence of Eqn. 13.18 has been made for convenience, but there is some justification for it, as we show in Section 13.7. Wilson’s equation becomes

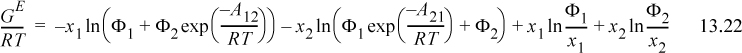
Algebraic rearrangement of Wilson’s equation results in the form that is usually cited,

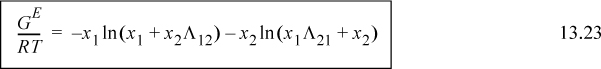
For a binary system, the activity coefficients from the Wilson equation are:

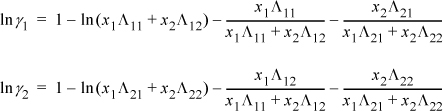
Noting that Λ₁₁ = Λ₂₂ = 1, and looking back at Eqn. 13.6, we can also see that for the first equation . We can rearrange this expression to obtain the slightly more compact relation:

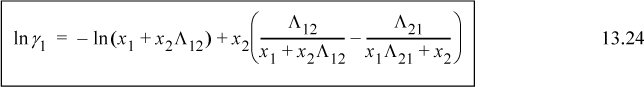
Similar rearrangement of the second expression gives:

 Wilson’s equation.

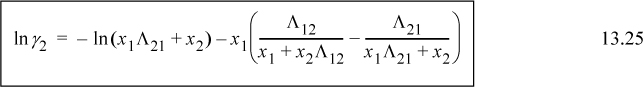
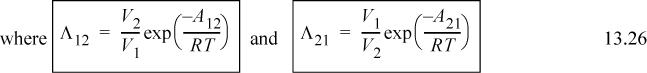
 Parameters for the Wilson equation, A_ji. Note that the literature values often include energy units. Use the correct R!

 Wilson’s equation is incapable of representing LLE.

One limitation of Wilson’s equation is that it is unable to model liquid-liquid equilibria, but it is reasonably accurate for modeling the liquid phase when correlating the vapor liquid equilibria.

Extending Eqn. 13.23 to a multicomponent solution,

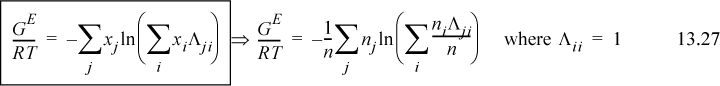
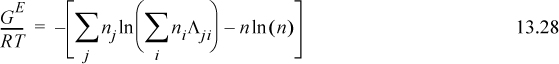
To determine activity coefficients, the excess Gibbs energy is differentiated. Differentiating the last term,

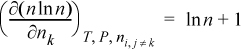
and letting “sum” stand for the summation of Eqn. 13.28, and combining,

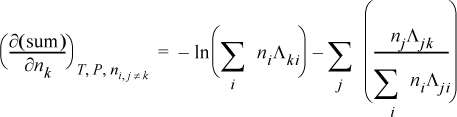
combining,

---

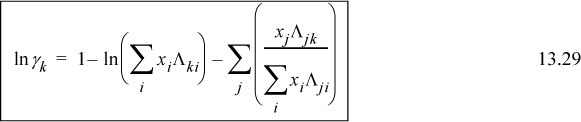
Example 13.3. Application of Wilson’s equation to VLE

For the binary system n-pentanol(1) + n-hexane(2), the Wilson equation constants are A₁₂ = 1718 cal/mol, A₂₁ = 166.6 cal/mol. Assuming the vapor phase to be an ideal gas, determine the composition of the vapor in equilibrium with a liquid containing 20 mole% n-pentanol at 30°C. Also calculate the equilibrium pressure. ; .

Solution

From CRC,

ρ₁ = 0.8144 g/ml (1mole/88g) ⇒ V₁ = 108 cm³/mole

ρ₂ = 0.6603 g/ml (1mole/86g) ⇒ V₂ = 130 cm³/mole

Note: ρ₁ and ρ₂ are functions of T but ρ₁/ρ₂ ≈ const. ⇒ V₂/V₁ = 1.205 assumed at all T.

Utilizing Eqn. 13.26,

Λ₁₂ = 1.205 exp(– 1718/1.987/303) = 0.070; Λ₂₁ = 1/1.205 exp(– 166.6/1.987/303) = 0.629

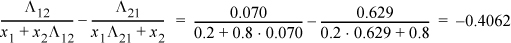
In γ₁ = 1.0408 ⇒ γ₁ = 2.822;    In γ₂ = 0.1584 ⇒ γ₂ = 1.172

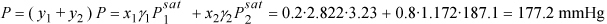
y₁ = x₁γ₁P^sat/P = 0.2·2.822·3.23/177.2 = 0.0103