Most systems encountered in chemical processes and formulations are multicomponent. If the application requires bypassing an azeotrope, a third component (called an entrainer) might be added. If a biomembrane is to be penetrated by a pharmaceutical treatment, the formulation must at least account for water, the pharmaceutical, the biomembrane, and any additive. The output of a simple reaction like A + B → C would mean that at least three components must be separated if conversion was less than 100%. These examples and more lead to the conclusion that a multicomponent solution model is a necessity.
Unfortunately, the van Laar model makes the assumption that V2/V1 can be treated as an adjustable parameter. While this is fine for a binary mixture, it becomes problematic for a ternary mixture because knowing V2/V1 and V3/V2 means that V3/V1 must be implied. The normal procedure for the van Laar model would fit the binaries for 2-1, 3-2, and 3-1 independently, however. The likelihood of achieving a consistent value of V3/V1 from such a fit is practically zero.
On the other hand, the simple relation of the Scatchard-Hildebrand theory to the van der Waals equation permits a simple extension to multicomponent systems. The derivation of this extension is given by practice problem 12.4. The result is
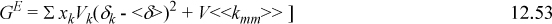
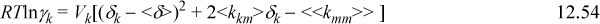
where <δ> = ΣΦjδj; <<kmm>> = ΣΦiδi<kim>; and <kim> = ΣΦjδj<kij>.
The SSCED model is similar to the Scatchard-Hildebrand model by design. This similarity guarantees that the algebra extending to multicomponent mixtures is identical, giving
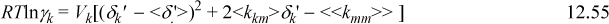
where <δ.′> = ΣΦjδj’<<kmm>> = ΣΦiδi’<kim>; and <kim> = ΣΦjδj’<kij>.
At first sight, the notation may seem confusing. The following example clarifies the necessary summations.
Example 12.7. Multicomponent VLE using the SSCED model
A partial condenser is generally indicated when distilling a stream that has a light gas impurity, even if the gas is dilute. A total condenser is impractical because of the “noncondensable” gas. Of course, we know that it must condense at some sufficiently low temperature, but it is wasteful to cool the stream that far or reflux the light gas component. A partial condenser condenses just as much liquid as necessary to keep the column functioning then sends the remainder downstream as a vapor distillate product. Downstream, a second partial condenser will provide liquid and the remaining gas can be purged to a flare tower.
Fermentation of corn to form acetone (A), n-butanol (B), and ethanol (E) in water (W) followed by a drying step results in the stream below to be distilled.a Dissolved carbon dioxide (CO2) is a prevalent by-product of the fermentation process. Use the SSCED model and assume 2 bar pressure with splits of 99% ethanol and 2.8% water. Assume that acetone moderates the ethanol+water interaction to achieve this tops composition without an azeotrope interfering. You may estimate vapor pressures using the shortcut equation.
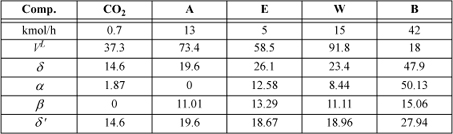
where δ’ has been computed from δ in accordance with Eqn. 12.50.
a. Estimate the flow rate and composition of the distillate based on the key component splits.
b. Estimate the dew temperature of the distillate stream as a preliminary estimate of the operating temperature in the partial condenser.
Solution
We will indicate the vapor outlet of the partial condenser stream as D.
a. E will be the light key, and W the heavy key. Everything lighter than the light key is assumed to go out the top, and everything heavier than the heavy key is assumed to go out the bottom. We estimate the boiling temperatures (K) at 2 bar in the first row. Technically, CO2 does not have a boiling temperature at 2 bar. Nevertheless, we apply the shortcut model here (at 351 K, where CO2 is supercritical) merely as an estimate, as suggested in the problem statement. Components are sorted in decreasing volatility to show that a split between E and W sends CO2 and A completely to distillate and B completely to the bottoms. The third row shows the consequent distillate (D) flows and fourth row shows the mole fractions.
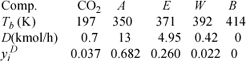
The tops composition of ethanol to water on a solvent-free basis is 4.95/(4.95+0.42) = 92%, which exceeds the azeotropic composition only slightly.
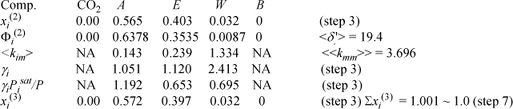
b. For the dew-temperature calculation, we use option (b) from Appendix C and refer to the step numbers. As an initial estimate, ![]() and assuming Raoult’s law (step 1),
and assuming Raoult’s law (step 1), ![]() gives
gives ![]() :
:

![]() Dew – temperature calculation.
Dew – temperature calculation.
In the last row, we divide xi(0) by Σxi(0) (the process is known as normalization), such that the mole fractions xi(0’) sum to one. To prepare for step 3, the SSCED model gives the values below for kij. For example, the value for ethanol + water is
kEW = (12.58 – 50.13)(13.29 – 15.06)/(4(18.67)27.94) = 0.0319
Similarly, kAE = 0.0184; kAW = 0.0896.
Finally, we are ready to apply the SSCED model. We drop butanol and CO2 from further calculations because their liquid compositions are zero. xi(1) is the result of the first iteration in which the γi are applied. xi(2) results from varying the temperature while assuming the γi are constant (even though the composition is changing slightly too). We are approximating to force xT = 1 to get a good T guess (step 5) for the next iteration.

where γA, γE, γW, <δ.′>, <kim>, and <<kmm>> are computed by Eqn. 12.55. For example,
<δ.′> = 0.6094(19.6) + 0.3710(18.67) + 0.0196(27.94)0.0319 = 19.4
<kEm> = 0.6094(19.6)0.0184 + 0.3710(18.67)0.0 + 0.0196(27.94)0.0319 = 0.239
<<kmm>> = 0.6094(19.6)0.177 + 0.3710(18.67)0.239 + 0.0196(27.94)1.294 = 4.478
γE = exp(58.5((18.67 – 19.4)2 + 2(0.239)18.67 – 4.478)/(8.314 . 351)) = 1.106
In going from xi(1’) to xi(2), we have varied the temperature assuming that the γi are unchanged. This must be validated with one final iteration at T = 354.88 K.
1. The liquid composition of less volatile components is enhanced in a partial condenser.
2. For this particular condenser, KW >KE means there is a limit to splitting W from E.
a. This problem is based on the AIChE 2009 National Student Design Competition, Richard L. Long Coordinator, AIChE New York (2008).
Noting that MAB is a special case of the SSCED model, the expression for the multicomponent SSCED model suggests a similar form for the MAB model.

The relation between the Margules form and the Redlich-Kister form suggests a similar relation.
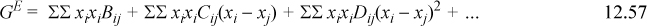
In this manner, we can envision extending many activity models to multicomponent applications.
The power to design formulations that solve practical problems generally involves multicomponent systems. Design requires synthesis of many fundamental principles into a working toolbox as well as creative thinking. If we want to disperse an oil spill, we should consider the fate of the additive as well as the oil. After the oil is dispersed, where will the additive go? What is its toxicity? If we want to circumvent an azeotrope, where will the entrainer go? Should it be more volatile or less volatile than the key components? How should its molecular properties relate to those of the key components? What about the volatility of a solvent to remove paint? What about the solvent’s water solubility? The multicomponent SSCED perspective empowers us to think creatively about these kinds of problems.
Example 12.8. Entrainer selection for gasohol production
The ethanol + water system has a well-known azeotrope at 89.4 mol% ethanol and 353 K, frustrating efforts to distill fuel grade ethanol cheaply and easily. Industrially, the azeotrope is broken using adsorption. Another strategy is to add a third component (an “entrainer”) that reduces the activity coefficient of the water. In this way, the relative volatility of ethanol to water can remain greater than one. Noting that activity coefficients pertain to the liquid phase, our entrainer should stay in the liquid phase. In other words, it should be less volatile than either key component. We can envision pouring it into the top of the distillation column and letting it trickle down. This process is called extractive distillation. We would like to use as little entrainer as possible and it should not form another azeotrope with water. One suggested entrainer is 2-pyrrolidone, for which the key properties are given below. You can assume the shortcut VP model for 2-pyrrolidone and SSCED predictions for kij interactions with 2-pyrrolidone. How much 2-pyrrolidone would be needed to keep the relative volatility greater than 1.1 at 99mol% ethanol? Can you suggest any other prospective entrainers based on their molecular structure?
Molecular properties for 2-pyrrolidone are

Solution
Noting that azeotropes are sensitive to vapor pressure, we should use the Antoine constants from Appendix E for ethanol and water. The vapor pressure of the entrainer is less important because it must be substantially lower than that of water to prevent another azeotrope. The SSCED predicted value of k12 = 0.0319 fails to reproduce the experimentally observed azeotrope, but a value of k12 = 0.058 gives an azeotrope with xE = 0.894 and 353 K. Checking the relative volatility at xE = 0.99 and 353 K we find αLH = 0.94. We should add entrainer until αLH = 1.1.
We can assume T = 353 K for now, so the vapor pressure ratio stays constant. We can check our result at the bubble temperature of the final formulated composition. Recalling the definition of relative volatility from Section 10.6 and substituting modified Raoult’s law,
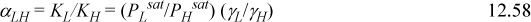
From the Antoine equation, PLsat/PHsat = 2.03. Therefore, we seek γL/γH > 1.1/2.03 = 0.542.
Taking a basis of 1 mole of ethanol (and 0.0101 water), increasing the ratio of 2-pyrrolidone (P) to ethanol to 0.05 gives a final composition of {0.9433, 0.0095, 0.0472} for {xE, xW, xP}. This gives a value of αLH = 2.03(1.001/2.075) = 1.11. Setting the pressure to 0.101 MPa and finding the bubble temperature gives T = 352.6, so the temperature is altered very little.
Another candidate for entrainer might be ethylene glycol. From its molecular structure, it is similar to half ethanol and half water. Following the same procedure, we find that a final composition of {0.8532, 0.0086, 0.1382} is required to achieve the same αLH. This is roughly a factor of 3 for entrainer on a mole basis or a factor of 2 on a weight basis. 2-pyrrolidone is predicted to be superior because of the large value for its basicity, larger than water’s. This causes the kij parameters with 2-pyrrolidone to be negative, so less is needed. Glycol is less effective.
Leave a Reply