We noted in Example 11.1 a shortcoming in the one-parameter model’s representation of the skewness of experimental excess Gibbs energy. In principle, adjusting both the magnitude and skewness of GE is possible with a two-parameter model equation. The mathematical relations in Sections 11.3–11.5 liberate us to conjecture freely about forms of GE that may fit any given set of VLE data. Based on any model, developing working equations for activity coefficients is a straightforward matter of taking derivatives. These are the considerations behind many empirical models like the Redlich-Kister and Margules two-parameter models.
Many models can be rewritten in the Redlich-Kister form given as9
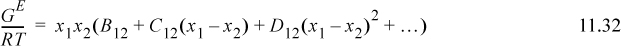
Two-Parameter Margules Model
The two-parameter Margules model is a simplification of the Redlich-Kister,

where we relate the constants to the Redlich-Kister via A21 = B12 + C12, A21 = B12 – C12, and D12 = 0. The constants A21 and A12 are fitted to experiment as we show below. Note that if A21 = A12, the expression reduces to the one-parameter model. The expression for the activity coefficient of the first component can be derived as
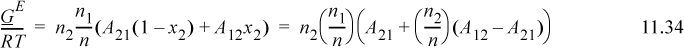
Applying Eqn. 11.28 for i = 1, and using the product rule on n1/n = n1(1/n) and n2/n = n2(1/n),
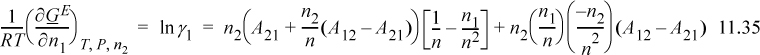
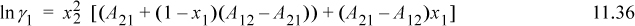
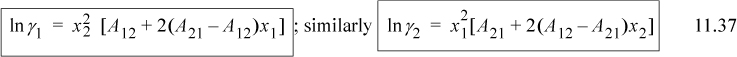
![]() Actcoeff.xlsx, sheet Margules; gammaModels/Marg2P.m.
Actcoeff.xlsx, sheet Margules; gammaModels/Marg2P.m.
The two parameters can be fitted to a single VLE measurement using
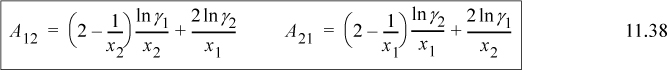
where the activity coefficients are calculated from the VLE data. Care must be used before accepting the values from Eqn. 11.38 applied to a single measurement because experimental errors can occasionally result in questionable parameter values.
Example 11.5. Fitting one measurement with the two-parameter Margules equation
We mentioned following Example 11.2 that a single experiment could be used more effectively with the two-parameter model. Apply Eqn. 11.38 to the two activity coefficients values calculated in Example 11.1 and estimate the two parameters. This is an example of a Stage II calculation.
Solution
From Example 11.1, x1 = 0.6369, x2 = 0.3631, and γ1 = 1.118, γ2 = 2.031. From Eqn. 11.38,
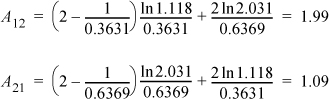
The parameters from Example 11.5 provide the representation of GE shown in Fig. 11.3. Using the concepts from earlier examples along with Eqn. 11.37 for the activity coefficients, bubble-pressure calculations across the composition range (Stage III calculations) result in the curve of Fig. 11.5 designated as the two-parameter model.
Example 11.6. Dew pressure using the two-parameter Margules equation
Use the parameters of Example 11.5 to predict the dew-point pressure and liquid composition for the 2-propanol(1) + water(2) system at T = 30°C, y1 = 0.4, and compare with Fig. 11.5. Use the vapor pressures, ![]() ,
, ![]() .
.
Solution
We will apply the procedure in Appendix C and refer to step numbers there.
Step 1. Refer to Chapter 10, P = 1/(0.4/60.7 + 0.6/32.1) = 39.55 mmHg, x1 = 0.4(39.55)/60.7 = 0.26. We skip Step 2 the first time.
Step 3. Using parameters from Example 11.5 in Eqn. 11.37, γ1 = exp(0.742(1.99 – 1.8(0.26)))=2.30; γ2 = exp(0.262(1.09 + 1.8(0.74)))=1.18.
Step 4. P = 1/(0.4/(2.3·60.7) + 0.6/(1.18·32.1)) = 53.46 mmHg.
Note the jump in P compared to Step 1 for the first loop.
Step 5. x1 = 0.4(53.46)/(2.3·60.7) = 0.153. Continuing the loop:
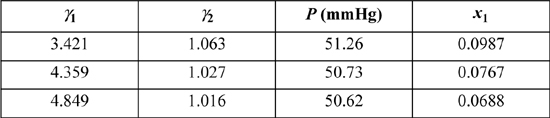
Continuing for several more iterations with four digits, P = 50.63 mmHg, and x1 = 0.0649. The calculations agree favorably with Fig. 11.5. The dew calculations are consistent with a bubble calculation at x1 = 0.0649.
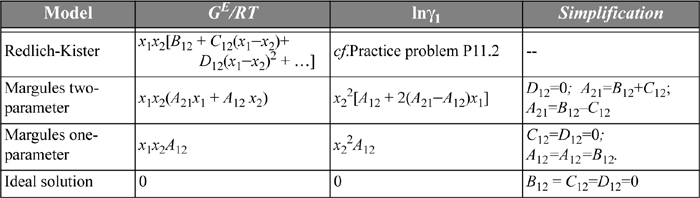
Because this is a long chapter, we summarize the relations between the activity coefficient models developed thus far in Table 11.2.
Table 11.2. Summary of Empirical Activity Models and Simplifications Relative to the Redlich-Kister
Leave a Reply