Summary

The concepts in this chapter are relatively simple but far-reaching. A simple extension of the chain rule to multicomponent systems led to the equilibrium constraint for multicomponent multiphase equilibria. A simple application of the entropy of mixing derived in Chapter 4 led to the ideal solution model, Gibbs energy for a component in a mixture, and fugacity for a component in a mixture. This simple solution model enabled us to demonstrate the computational procedures for dew points, bubble points, and flashes.

In the remaining chapters of Unit III we proceed in a manner that is extremely similar. We propose a solution model and apply the equilibrium constraint to derive an expression for the K-ratios. Then we follow exactly the same computational procedures as developed here. The primary difference is the increasing level of sophistication incorporated into each solution model. Thus, the chapters ahead focus increasingly on the detailed description of the molecular interactions and the impacts of assumptions on the accuracy of the resultant solution models.

In this context, this chapter represents one iteration in the typical sequence of “observe, predict, test, and evaluate.” We observed that isothermal mixtures boil at higher pressures when more volatile components were present. We predicted that the bubble pressure varies linearly in mole fraction between the vapor pressures of the components (Raoult’s law). We tested these predictions by checking the linearity of several mixtures. We evaluated the assumptions implicit in Raoult’s law by extending the fundamental thermodynamic principles to mixtures. Successive iterations involve repeating this sequence, following up on clues from the previous evaluation.

Important Equations

We defined the K-ratio.

Raoult’s law is an important equation, but we have also seen that it has limited applicability.

We developed methods to calculate bubble, dew, and flash conditions summarized in Table 10.1 on page 373. We developed the relation for the relative volatility,

We discussed how the relative volatility varies dramatically with composition in an azeotropic system, approaching 1 at the azeotrope, and creating challenges. These variations undermine the utility of Raoult’s law and the use of shortcut design equations for azeotropic systems.

For phase equilibria, including liquid-liquid equilibria, the fugacities of a component are equal,

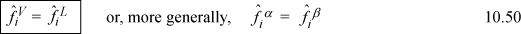
where α and β indicate different phases, whether vapor, liquid(s), or solid. This is the starting point throughout Unit III. As we applied the generalized approach, we found

and for an ideal solution,

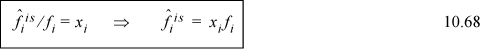
Two final equations that form the basis for future derivations are

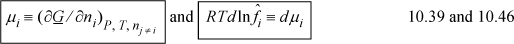
Through these equations, we can infer the fugacities of components in any solution, no matter how complex, by building a model for Gibbs energy. This is the subject of upcoming chapters. Models of the Gibbs energy may range from crudely empirical to sophisticated molecular analyses.