Generalization of pure-component principles to multicomponent systems requires that we consider how the thermodynamic properties change with respect to changes in the amounts of individual components. For a pure fluid, the natural properties were simply a function of two state variables. In multicomponent mixtures, these energies and the entropy also depend on composition.
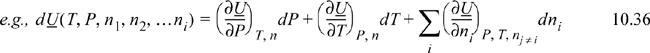
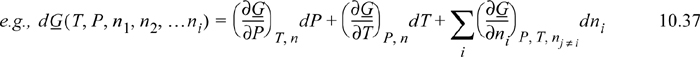
![]() These equations extend the use of calculus from Chapter 6 to composition variables.
These equations extend the use of calculus from Chapter 6 to composition variables.
Note that these equations follow the mathematical rules developed in Chapter 6. Each term on the right-hand side consists of a partial derivative with respect to one variable, with all other variables held constant. The summation is simply a shorthand method to avoid writing a term for each component. The subscript nj ≠ i means that the moles of all components except i are held constant. In other words, for a ternary system, ((∂U)/(∂n1))P, T, nj ≠ i means the partial derivative of U with respect to n1 while holding P, T, n2, and n3 constant. For phase equilibria where P and T are manipulated, Eqn. 10.37 is more useful than Eqn. 10.36 because the Gibbs energy is a natural function of P and T. At constant moles and composition of material, the mixture must follow the same constraints as a pure fluid. That is, the state is dependent on only two state variables if we keep the composition constant.
⇒ (∂G/∂P)T,n = V and (∂G/∂T)P,n = – S;
These complicated-looking derivatives are really fundamental properties; therefore, we can rewrite Eqn. 10.37 as
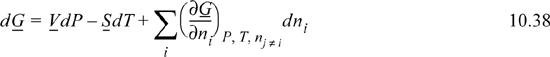
The quantity (∂G/∂ni)P, T, nj ≠ i tells us how the total Gibbs energy of the mixture changes with an infinitesimal change in the number of moles of species i, when the number of moles of all other species fixed, and at constant P and T. The quantity (∂G/∂ni)P, T, nj ≠ i will become very important in our later discussion. so we give it a name, called the chemical potential, and give it a symbol.

We commonly write
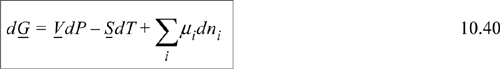
Partial Molar Properties
Another name for the special derivative of Eqn. 10.39 is the partial molar Gibbs energy. We may generalize the form of the derivative and apply it to other properties. For any extensive thermodynamic property M, we may write ![]() . Note that T, P, and nj ≠ i are always held constant for a partial molar property. The overbar indicates a partial molar quantity, that is, for total volume V, the quantity (∂V/∂ni)T,P,nj≠i is called the partial molar volume and given the symbol
. Note that T, P, and nj ≠ i are always held constant for a partial molar property. The overbar indicates a partial molar quantity, that is, for total volume V, the quantity (∂V/∂ni)T,P,nj≠i is called the partial molar volume and given the symbol ![]() . Suppose we were considering a mixture of 500 red balls of size σR and 700 blue balls of size σB. How would the total volume change if we added one more red ball, keeping 700 blue balls? This is a finite difference example of the derivative called the partial molar volume of red balls. A special mathematical result of the differentiation is that we may write at constant temperature and pressure:
. Suppose we were considering a mixture of 500 red balls of size σR and 700 blue balls of size σB. How would the total volume change if we added one more red ball, keeping 700 blue balls? This is a finite difference example of the derivative called the partial molar volume of red balls. A special mathematical result of the differentiation is that we may write at constant temperature and pressure:
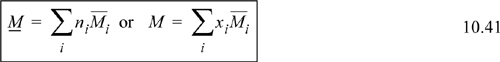
![]() Partial molar quantities provide a mathematical way to assign the overall mixture property according to composition expressed in moles or mole fractions.
Partial molar quantities provide a mathematical way to assign the overall mixture property according to composition expressed in moles or mole fractions.
As a result, we may write
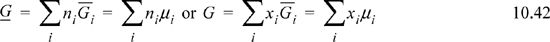
We will return to these basic equations as we develop more relations for mixtures.
The chemical potential becomes an important term for each of the key properties, U, H, A, and G, because they are all related by an appropriate Legendre transform as shown in the following table. The constraints on the derivative are important. For example, (∂U/∂ni)P, T, nj ≠ i in Eqn. 10.36 is not equal to (∂U/∂ni)S, V, nj ≠ i = μi in the first line of the table.
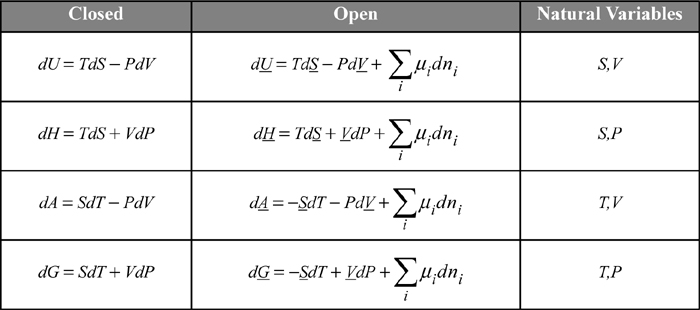
The open systems equations can be developed using the energy and entropy balances from the early chapters as shown in an online supplement.
Equilibrium Criteria
For equilibrium at constant T and P, the Gibbs energy is minimized and mathematically the minimum means dG = 0 at equilibrium. Therefore, Eqn. 10.38 is equal to zero at a minimum, since dT and dP are zero, and for a closed system all dni are zero. Thus,
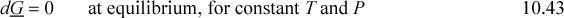
This equation applies to whatever system we define. Suppose we define our system to consist of two components (e.g,. EtOH + H2O) distributed between two phases (e.g., vapor and liquid), dG = dGL + dGV = 0, and at constant T and P, the moles may redistribute between the two phases, by Eqn. 10.40 for both phases:
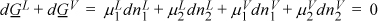
But if component 1 leaves the liquid phase then it must enter the vapor phase (and similarly for component 2) because the overall system is closed.
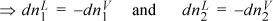
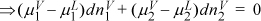
The only way to make this equal to zero in general is:

![]() The chemical potential of each component must be the same in each phase at equilibrium.
The chemical potential of each component must be the same in each phase at equilibrium.
Setting the chemical potentials and T and P in each of the phases equal to each other provides a set of constraints (simultaneous equations) which may be solved for phase compositions provided we know the dependency of the chemical potentials on the phase compositions. Suppose the functions GL (x,T,P) and GV (y,T,P) are available for a binary system. Then
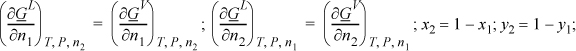
which gives four equations with four unknowns (x1, x2, y1, y2) that we can solve, in principle.11 The first two equations are simply the equivalency of chemical potentials in the two phases.
Chemical Potential of a Pure Fluid
In Chapter 9, we showed the equilibrium constraint for a pure fluid is equality of the molar Gibbs energy for each of the phases (cf. Eqn. 9.3). How does this relate to Eqn. 10.44?
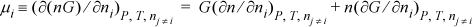
For a pure fluid, there is only one component, so dni = dn, and since G(T,P) is intensive, then n(∂G/∂n)T,P = 0. Also (∂n/∂ni)T,P = 1 by Eqn. 6.13. Therefore,

![]() The chemical potential of a pure fluid is simply the molar Gibbs energy.
The chemical potential of a pure fluid is simply the molar Gibbs energy.
That is, the chemical potential of a pure fluid is simply the molar Gibbs energy. Pure components can be considered as a special case of the same general statement of the equilibrium constraint.
Component Fugacity
We introduced fugacity in Chapter 9. The chemical potential constraint is sufficient for solving any phase equilibrium problem, but the most popular engineering approach for actual computations makes use of the concept of fugacity. Fugacity is more “user-friendly” than “chemical potential” or “partial molar Gibbs energy.” We have seen in Chapter 9 that the fugacity is the same as the pressure for an ideal gas, and that the fugacity is close to the vapor pressure for a liquid. Engineers use benchmarks such as these as guidelines for estimating fugacities and double-checking calculations. Fuga– comes from a Latin noun meaning flight, fleeing, or escape. The suffix –ity comes from a root meaning “character.” Thus, fugacity was invented to mean flight-character, commonly called “escaping tendency.” When phases are in equilibrium, the component moves (“escapes”) from the phase where it has the higher fugacity to the phase where it has the lower fugacity until the fugacities are equal in both phases.12
Let us generalize our pure component fugacity relations to apply to components in mixtures: At constant T, we defined RTdlnf ≡ dG (Eqn. 9.19) which can be generalized to define the fugacity of a component in a mixtures as

![]() Fugacity is another way to express the chemical potential that is used more widely in engineering than chemical potential.
Fugacity is another way to express the chemical potential that is used more widely in engineering than chemical potential.
where ![]() is the fugacity of component i in a mixture and μi is the chemical potential of the component. In the limit as the composition approaches purity, these properties become equal to the pure component values. A caret is used in the symbol for the fugacity of a component. The component fugacity is not a partial molar property, so the overbar cannot be used.
is the fugacity of component i in a mixture and μi is the chemical potential of the component. In the limit as the composition approaches purity, these properties become equal to the pure component values. A caret is used in the symbol for the fugacity of a component. The component fugacity is not a partial molar property, so the overbar cannot be used.
![]() Carets (^) are used to denote component properties in mixtures for f while without a caret the property is the pure component f. When working with μ, the meaning is inferred from the context of the situation.
Carets (^) are used to denote component properties in mixtures for f while without a caret the property is the pure component f. When working with μ, the meaning is inferred from the context of the situation.
Equality of Fugacities as Equilibrium Criteria
The equality of chemical potentials at equilibrium can easily be reinterpreted in terms of fugacity in a manner analogous to our methods for pure components from Eqn. 10.44:

By integrating Eqn. 10.46 as a function of composition at fixed T from a state of pure i to a mixed state, we find

where μi,pure and fi are for the pure fluid at the system temperature. Writing an analogous expression for the liquid phase, and equating the chemical potentials using Eqn. 10.47, we find


Note: Eqn. 10.47 or 10.50 becomes the starting point for all phase-equilibrium calculations. Therefore, we need to develop the capability to calculate chemical potentials or fugacities of components in vapor, liquid, and solid mixtures. Here we briefly introduce the framework for calculating the fugacities of components before we begin the direct calculations.
Eqn 10.50 does not look much like Raoult’s law, which was our motivation for exploring the thermodynamics of mixtures. To make this final connection between Raoult’s law and Eqn. 10.50, we need to understand how energy and volume affect component fugacities.
Leave a Reply