Introduction to Phase Diagrams

Before we delve into the details of calculating phase equilibria, let us introduce elementary concepts of common vapor-liquid phase diagrams. For a pure fluid, the Gibbs phase rule shows vapor-liquid equilibrium occurs with only one degree of freedom, F = C – P + 2 = 1 – 2 + 2 = 1. At one atmosphere pressure, vapor-liquid equilibria will occur at only one temperature—the normal boiling point temperature. However, with a binary mixture, there are two degrees of freedom, F = 2 – 2 + 2 = 2. For a system with fixed pressure, phase compositions and temperature can both be varied over a finite range when two phases coexist. Experimental data for experiments of this type are usually presented as a function of T and composition on a plot known as a T-x-y diagram, such as that shown qualitatively in Fig. 10.1. At fixed temperature, pressure and composition may vary in a binary mixture and obtain data to create a P-x-y diagram as shown also in Fig. 10.1. The region where two phases coexist is shown by the area enclosed by the curved lines on either plot and is known as the phase envelope.¹ On the T-x-y diagram, the vapor region is at the top (raising T at fixed P causes vaporization of liquid). On the P-x-y diagram, the vapor region is at the bottom (lowering P at fixed T causes vaporization of liquid). Note that the intersections of the phase envelope with the ordinate scales at the pure component compositions give the pure component saturation temperatures on the T-x-y diagram, and the pure component vapor (saturation) pressures on the P-x-y diagram. Therefore, significant information about the shape of the diagram can often be deduced with a single mixture data point when combined with the pure component end points. Qualitatively, the shape of the P-x-y diagram can be found by inverting the T-x-y, and vice versa.² Customarily, for binary systems in the separations literature, the more volatile component composition is plotted along the abscissa in mole fraction or percent.

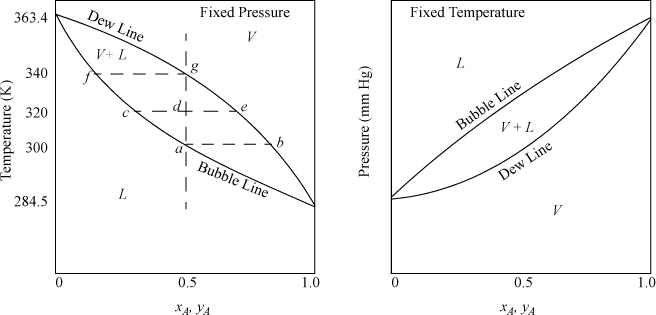
Figure 10.1. Illustration of T-x-y (left) and P-x-y (right) diagrams.

The ability to quickly read phase diagrams is an essential skill.

The lower curve on the T-x-y diagram is next to the liquid region, and it is known as the bubble line. The bubble-temperature line gives the boiling temperature of the mixture as a function of composition at the specified pressure. The upper curve is next to the vapor region, and is known as the dew line. The two lines meet at the axes if the conditions are below the critical pressure of both components. At a given composition, the temperature along the bubble line is the temperature where an infinitesimal bubble of vapor coexists with liquid. Thus, at an over-all composition of 50 mole% A, the system of Fig. 10.1 at fixed pressure is 100% liquid below 300 K at the pressure of the diagram. As the temperature is raised, the overall composition is constrained to follow the vertical dashed line constructed on the diagram, and the first vapor bubble forms at the intersection of the bubble line at 300 K at point a, which is known as the bubble temperature for a 50 mole% mixture at the system pressure. Phase compositions at a given P and T may be found by reading the compositions from intersections of the bubble and dew lines with horizontal lines constructed on the diagram, such as the dashed line at 300 K. For our example at the bubble temperature, the liquid phase will be 50 mole% A because the first bubble of vapor has not yet caused a measurable change in the liquid composition. The vapor phase composition coexisting at the bubble-point temperature will be 80 mole% A (point b). As the temperature is increased to 320 K, the overall mixture is at point d, the liquid phase will be 30 mole% A (point c), and the vapor phase will be 70 mole% A (point e). Suppose we start an experiment with a 50 mole% mixture at 350 K, where the mixture is 100% vapor. As the temperature is lowered, the dew temperature is encountered at 340 K for the 50 mole% mixture at system pressure (point g), and the first drop of liquid is formed which is about 20 mole% A (point f). Note that the bubble and dew temperatures are composition-dependent. For example, the bubble temperature of a 30 mole% mixture is 320 K (point c), and the bubble temperature of a 20 mole% mixture is 340 K (point f). Similar discussion could be presented for the dew temperatures. The bubble and dew-point discussions could also be presented on the pressure diagram, but in this case we would refer to the bubble and dew pressures. Note that the relative vertical locations of the bubble- and dew lines are flipped on the two diagrams. The horizontal dotted lines connecting coexisting compositions are tie lines.

When we speak of composition in a two-phase mixture, we must be clear about which phase we are discussing. We use x to denote a liquid phase mole fraction, y to denote a vapor phase mole fraction, and z to denote an overall mole fraction.³ For the example, we have been discussing using a 50 mole% mixture: At the bubble point of 300 K we have z_A = 0.5, x_A = 0.5, y_A = 0.8; at 320 K we have z_A = 0.5, x_A = 0.3, y_A = 0.7; At 340 K we have z_A = 0.5, x_A = 0.20, y_A = 0.5. At 320 K, the system is in the two-phase region, and we may use the compositions of the vapor and liquid phases, together with an overall mass balance, to calculate the fraction of the overall mixture that is vapor or liquid. This is known as a flash calculation. If the initial number of moles is denoted by F, and it separates into L moles of liquid and V moles of vapor, the overall mole balance is F = L + V, which can be written 1 = L/F + V/F. The A component balance is z_AF = y_AV + x_AL, which can be written z_A = y_A · V/F + x_A · L / F. Combining the two balances to eliminate V/F, the percentage that is liquid will be