9.1. The heat of fusion for the ice-water phase transition is 335 kJ/kg at 0°C and 1 bar. The density of water is 1g/cm3 at these conditions and that of ice is 0.915 g/cm3. Develop an expression for the change of the melting temperature of ice as a function of pressure. Quantitatively explain why ice skates slide along the surface of ice for a 100 kg hockey player wearing 10 cm x 01 cm blades. Can it get too cold to ice skate? Would it be possible to ice skate on other materials such as solid CO2?
9.2. Thermodynamics tables and charts may be used when both H and S are tabulated. Since G = H – TS, at constant temperature, ΔG = RT ln(f2/f1) = ΔH – TΔS. If state 1 is at low pressure where the gas is ideal, then f1 = P1, RT ln(f2/P1) = ΔH – TΔS, where the subscripts indicate states. Use this method to determine the fugacity of steam at 400°C and 15 MPa. What value does the fugacity coefficient have at this pressure?
9.3. This problem reinforces the concepts of phase equilibria for pure substances.
a. Use steam table data to calculate the Gibbs energy of 1 kg saturated steam at 150°C, relative to steam at 150°C and 50 kPa (the reference state). Perform the calculation by plotting the volume data and graphically integrating. Express your answer in kJ. (Note: Each square on your graph paper will represent [pressure·volume] corresponding to the area, and can be converted to energy units.)
b. Repeat the calculations using the tabulated enthalpies and entropies. Compare your answer to part (a).
c. The saturated vapor from part (a) is compressed at constant T and 1/2 kg condenses. What is the total Gibbs energy of the vapor liquid mixture relative to the reference state of part (a)? What is the total Gibbs energy relative to the same reference state when the mixture is completely condensed to form saturated liquid?
d. What is the Gibbs energy of liquid water at 600 kPa and 150°C relative to the reference state from part (a)? You may assume that the liquid is incompressible.
e. Calculate the fugacities of water at the states given in parts (a) and (d). You may assume that f = P at 50 kPa.
9.4. Derive the formula for fugacity according to the van der Waals equation.
9.5. Use the result of problem 9.4 to calculate the fugacity of ethane at 320 K and at a molar volume of 150 cm3/mole. Also calculate the pressure in bar.
9.6. Calculate the fugacity of ethane at 320 K and 70 bar using:
a. Generalized charts
b. The Peng-Robinson equation
9.7. CO2 is compressed at 35°C to a molar volume of 200 cm3/gmole. Use the Peng-Robinson equation to obtain the fugacity in MPa.
9.8. Use the generalized charts to obtain the fugacity of CO2 at 125°C and 220 bar.
9.9. Calculate the fugacity of pure n-octane vapor as given by the virial equation at 580 K and 0.8 MPa.
9.10. Estimate the fugacity of pure n-pentane (C5H12) at 97°C and 7 bar by utilizing the virial equation.
9.11. Develop tables for H, S, and Z for N2 over the range Pr = [0.5, 1.5] and Tr = [Trsat, 300 K] according to the Peng-Robinson equation. Use the saturated liquid at 1 bar as your reference condition for H = 0 and S = 0.
9.12. Develop a P-H chart for saturated liquid and vapor butane in the range T = [260, 340] using the Peng-Robinson equation. Show constant S lines emanating from saturated vapor at 260 K, 300 K, and 340 K. For an ordinary vapor compression cycle, what would be the temperature and state leaving an adiabatic, reversible compressor if the inlet was saturated vapor at 260 K? (Hint: This is a tricky question.)
9.13. Compare the Antoine and shortcut vapor-pressure equations for temperatures from 298 K to 500 K. (Note in your solution where the equations are extrapolated.) For the comparison, use a plot of log10Psat versus 1/T except provide a separate plot of Psat versus T for vapor pressures less than 0.1 MPa.
a. n-Hexane
b. Acetone
c. Methanol
d. 2-propanol
e. Water
9.14. For the compound(s) specified by your instructor in problem 9.13, use the virial equation to predict the virial coefficient for saturated vapor and the fugacity of saturated liquid. Compare the values of fugacity to the vapor pressure.
9.15. Compare the Peng-Robinson vapor pressures to the experimental vapor pressures (represented by the Antoine constants) for the species listed in problem 9.13.
9.16. Carbon dioxide can be separated from other gases by preferential absorption into an amine solution. The carbon dioxide can be recovered by heating at atmospheric pressure. Suppose pure CO2 vapor is available from such a process at 80°C and 1 bar. Suppose the CO2 is liquefied and marketed in 43-L laboratory gas cylinders that are filled with 90% (by mass) liquid at 295 K. Explore the options for liquefaction, storage, and marketing via the following questions. Use the Peng-Robinson for calculating fluid properties. Submit a copy of the H-U-S table for each state used in the solution.
a. Select and document the reference state used throughout your solution.
b. What is the pressure and quantity (kg) of CO2 in each cylinder?
c. A cylinder marketed as specified needs to withstand warm temperatures in storage/transport conditions. What is the minimum pressure that a full gas cylinder must withstand if it reaches 373 K?
d. Consider the liquefaction process via compression of the CO2 vapor from 80°C, 1 bar to 6.5 MPa in a single adiabatic compressor (ηC = 0.8). The compressor is followed by cooling in a heat exchanger to 295 K and 6.5 MPa. Determine the process temperatures and pressures, the work and heat transfer requirement for each step, and the overall heat and work.
e. Consider the liquefaction via compression of the CO2 vapor from 80°C, 1 bar to 6.5 MPa in a two-stage compressor with interstage cooling. Each stage (ηC = 0.8) operates adiabatically. The interstage pressure is 2.5 MPa, and the interstage cooler returns the CO2 temperature to 295 K. The two-stage compressor is followed by cooling in a heat exchanger to 295 K and 6.5 MPa. Determine all process temperatures and pressures, the work and heat transfer requirement for each step, and the overall heat and work.
f. Calculate the minimum work required for the state change from 80°C, 1 bar to 295 K, 6.5 MPa with heat transfer to the surroundings at 295 K. What is the heat transfer required with the surroundings?
9.17. A three-cycle cascade refrigeration unit is to use methane (cycle 1), ethylene (cycle 2), and ammonia (cycle 3). The evaporators are to operate at: cycle 1, 115.6 K; cycle 2, 180 K; cycle 3, 250 K. The outlets of the compressors are to be: cycle 1, 4 MPa; cycle 2, 2.6 MPa; cycle 3, 1.4 MPa. Use the Peng-Robinson equation to estimate fluid properties. Use stream numbers from Fig. 5.11 on page 212. The compressors have efficiencies of 80%.
a. Determine the flow rate for cycle 2 and cycle 3 relative to the flow rate in cycle 1.
b. Determine the work required in each compressor per kg of fluid in the cycle.
c. Determine the condenser duty in cycle 3 per kg of flow in cycle 1.
d. Suggest two ways that the cycle could be improved.
9.18. Consider the equation of state
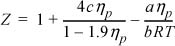
where ηp = b/V.
a. Determine the relationships between a, b, c and Tc, Pc, Zc.
b. What practical restrictions are there on the values of Zc that can be modeled with this equation?
c. Derive an expression for the fugacity.
d. Modify Preos.xlsx or Preos.m for this equation of state. Determine the value of c (+/- 0.5) that best represents the vapor pressure of the specified compound below. Use the shortcut vapor pressure equation to estimate the experimental vapor pressure for the purposes of this problem for the option(s) specifed by your instructor.
Leave a Reply