The Fundamental Property Relation

One equation underlies all the other equations to be discussed in this chapter. It is the combined energy and entropy balances for a closed system without shaft work. The only special feature that we add in this section is that we eliminate any references to specific physical situations. Transforming to a purely mathematical realm, we are free to apply multivariable calculus at will, transforming any problem into whatever variables seem most convenient at the time. Some of these relatively convenient forms appear frequently throughout the text, so we present them here as clear implications of the fundamental property relation changes in U.

The Fundamental Property Relation for dU in Simple Systems

We restrict our treatment here to systems without internal rigid, impermeable, or adiabatic walls, no internal temperature gradients, and no external fields. These restrictions comprise what we refer to as simple systems. This is not a strong restriction, however. Most systems can be treated as a sum of simple systems. Our goal is to transform the energy balance from extensive properties like heat and work to intensive (state) properties like density, temperature, and specific entropy. For this purpose, we may imagine any convenient physical path, recognizing that the final result will be independent of path as long as it simply relates state properties.

The energy balance for a closed simple system is

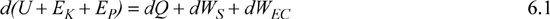
where E_K and E_P are the intensive kinetic and potential energies of the center of mass of the system. Eliminating all surface forces except those that cause expansion or contraction, because a simple system has no gradients or shaft work, and neglecting E_K and E_P changes by taking the system’s center of mass as the frame of reference,

Emphasizing the neglect of gradients, the reversible differential change between states is

but, by definition,

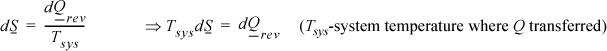
Since the system is simple, for the process to be internally reversible, the temperature must be uniform throughout the system (no gradients). So the system temperature has a single value throughout. On a molar basis, the fundamental property relation for dU is

 dU for a closed simple system.

The significance of this relation is that changes in one state variable, dU, have been related to changes in two other state variables, dS and dV. Therefore, the physical problem of relating heat flow and volume changes to energy changes has been transformed into a purely mathematical problem of the calculus of two variables. This transformation liberates us from having to think of a physical means of attaining some conversion of energy. Instead, we can apply some relatively simple rules of calculus given changes in S and V.

Auxiliary Relations for Convenience Properties

Because dU is most simply written as a function of S and V it is termed a natural function of S and V. We can express changes of internal energy in terms of other state properties (such as {P, T} or {T,V}), but when we do so, the expression always involves additional derivatives. We will show this in more detail in Example 6.11 on page 243. We also should explore the natural variables for the convenience properties.

We have defined enthalpy, H ≡ U + PV. Therefore, dH = dU + PdV + VdP = TdS – PdV + PdV + VdP,

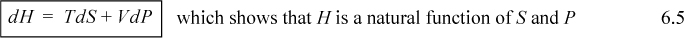
 dH for a reversible, closed simple system. Enthalpy is convenient when heat and pressure are manipulated.

The manipulation we have performed is known as a Legendre transformation. Note that {T, S} and {P, V} are paired in both U and the transform H. These pairs are known as conjugate pairs and will always stayed paired in all transforms.¹

Enthalpy is termed a convenience property because we have specifically defined it to be useful in problems where reversible heat flow and pressure are manipulated. By now you have become so used to using it that you may not stop to think about what the enthalpy really is. If you look back to our introduction of enthalpy, you will see that we defined it in an arbitrary way when we needed a new tool. The fact that it relates to the heat transfer in a constant-pressure closed system, and relates to the heat transfer/shaft work in steady-state flow systems, is a result of our careful choice of its definition.

We may want to control T and V for some problems, particularly in statistical mechanics, where we create a system of particles and want to change the volume (intermolecular separation) at fixed temperature. Situations like this also arise quite often in our studies of pistons and cylinders. Since U is not a natural function of T and V, such a state property is convenient. Therefore, we define Helmholtz energy A ≡ U – TS. Therefore, dA = dU – TdS – SdT = TdS – PdV – TdS – SdT,

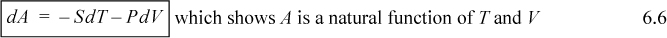
 Helmholtz energy is convenient when T, V are manipulated.

Consider how the Helmholtz energy relates to expansion/contraction work for an isothermal system. Equilibrium occurs when the derivative of the Helmholtz energy is zero at constant T and V. The other frequently used convenience property is Gibbs energy G ≡ U – TS + PV = A + PV = H – TS. Therefore, dG = dH – TdS – SdT = TdS + VdP – TdS – SdT.

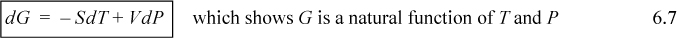
 Gibbs energy is convenient when T, P are manipulated.

The Gibbs energy is used specifically in phase equilibria problems where temperature and pressure are controlled. We find that for systems constrained by constant T and P, the equilibrium occurs when the derivative of the Gibbs energy is zero (⇒ driving forces sum to zero and Gibbs energy is minimized). Note that dG = 0 when T and P are constant (dT = 0, dP = 0). The Helmholtz and Gibbs energies include the effects of entropic driving forces. The sign convention for Helmholtz and Gibbs energies are such that an increase in entropy detracts from our other energies, A = U – TS, G = U – TS + PV. In other words, increases in entropy detract from increases in energy. These are sometimes called the free energies. The relation between these free energies and maximum work is shown in Section 4.12.

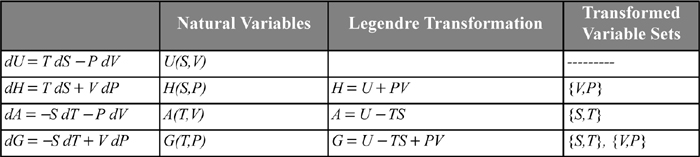
In summary, the common Legendre transforms are summarized in Table 6.1. We will use other Legendre transforms in Chapter 18.

Table 6.1. Fundamental and Auxiliary Property Relations

Often, students’ first intuition is to expect that energy is minimized at equilibrium. But some deeper thought shows that equilibrium based purely on energy would eventually reach a state where all atoms are at the minimum of their potential wells with respect to one another. All the world would be a solid block. On the other hand, if entropy was always maximized, molecules would spread apart and everything would be a gas. Interesting phenomena are only possible over a narrow range of conditions (e.g., 298 K) where the spreading generated by entropic driving forces balances the compaction generated by energetic driving forces. A greater appreciation for how this balance occurs should be developed over the next several chapters.