In a Rankine cycle, the vapor is superheated before entering the turbine. The superheat is adjusted to avoid the turbine blade erosion from low-quality steam. Similarly, the condenser completely reduces the steam to a liquid that is convenient for pumping.
In Fig. 5.2, state 4′ is the outlet state for a reversible adiabatic turbine. We use the prime (′) to denote a reversible outlet state as in the previous chapter. State 4 is the actual outlet state which is calculated by applying the efficiency to the enthalpy change.
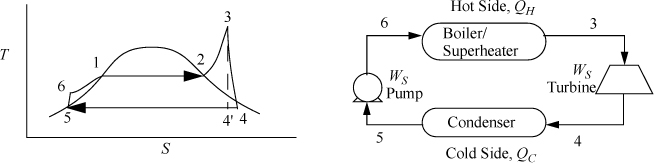
Figure 5.2. Rankine cycle.
![]() The prime denotes a reversible outlet state.
The prime denotes a reversible outlet state.
Because a real turbine always generates entropy, state 4 will always be to the right of 4′ on a T-S diagram. States 4 and 4′ can be inside or outside the phase envelope. Efficiencies are greater if state 4 is slightly inside the phase envelope because the enthalpy change will be larger for the same pressure drop due to the large enthalpy of vaporization; however, to avoid turbine blade damage, quality is kept above 90% in most cases.
Note in Fig. 5.2 that the superheater between the boiler and the turbine is not drawn, and only a single unit is shown. In actual power plants, separate superheaters are used; however, for the sake of simplicity in our discussions the boiler/superheater steam generator combination will be represented by a single unit in the schematic.
![]() Most plants will have separate boilers and superheaters. We show just a boiler for simplicity.
Most plants will have separate boilers and superheaters. We show just a boiler for simplicity.
Turbine calculation principles were covered in the last chapter. Now we recognize that the net work is the sum of the work for the turbine and pump and that some of the energy produced by the turbine is needed for the pump. In general, the thermal efficiency is given by:
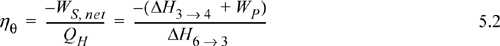
The boiler input can be calculated directly from the enthalpy out of the pump and the desired turbine inlet. The key steps are illustrated in Example 5.1.
A power plant uses the Rankine cycle. The turbine inlet is 500°C and 1.4 MPa. The outlet is 0.01 MPa. The turbine has an efficiency of 85% and the pump has an efficiency of 80%. Determine:
a. The work done by the turbine (kJ/kg)
b. The work done by the pump, the heat required, and the thermal efficiency;
c. The circulation rate to provide 1 MW net power output.
Solution
We will refer to Fig. 5.2 for stream numbers. The recommended method for solving process problems is to establish a table to record values as they are determined. In this text we will show values in the tables with bold borders if they have been determined by balance calculations. The turbine outlet can be read from the temperature table without interpolation. Cells with standard borders refer to properties determined directly from the problem statement
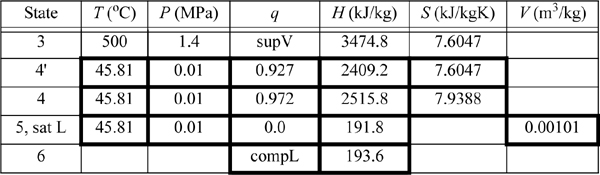
![]() Boldfaced table cells show calculations that were determined by balances. We follow this convention in the following examples.
Boldfaced table cells show calculations that were determined by balances. We follow this convention in the following examples.
Because the turbine inlet has two state variables specified, the remainder of the state properties are found from the steam tables and tabulated in the property table. We indicate a superheated vapor with “supV” compressed liquid with “compL.”
a. Stepping forward across the turbine involves the same specifications as part (c) of Example 4.13 on page 168. The properties from 4 and 4′ are transferred from that example to the property table. The work done is –959 kJ/kg.
b. The outlet of the condenser is taken as saturated liquid at the specified pressure, and those values are entered into the table. We must calculate ![]() and
and ![]() . So we need H6 and WS,pump which are determined by calculating the adiabatic work input by the pump to increase the pressure from state 5. Although the reversible calculation for the pump is isentropic, we may apply Eqn. 2.61 without direct use of entropy, and then correct for efficiency. For the pump,
. So we need H6 and WS,pump which are determined by calculating the adiabatic work input by the pump to increase the pressure from state 5. Although the reversible calculation for the pump is isentropic, we may apply Eqn. 2.61 without direct use of entropy, and then correct for efficiency. For the pump,
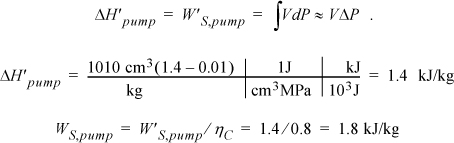
Thus, the work of the pump is small, resulting in H6 = 191.8 + 1.8 = 193.6 kJ/kg. The net work is W’S,net = –959.0 + 1.8 = 957.2 kJ/kg. The only source of heat for the cycle is the boiler/superheater. All of the heat input is at the boiler/superheater. The energy balance gives QH = (H3 – H6) = 3281.2 kJ/kg. The thermal efficiency is
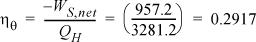
If we neglected the pump work, the efficiency would 29.23%. Note that the pump work has only a small effect on the thermal efficiency but is included for theoretical rigor.
c. For 1 MW capacity, ![]() , the circulation rate is
, the circulation rate is
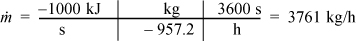
The cycle in Fig. 5.2 is idealized from a real process because the inlet to the pump is considered saturated. In a real process, it will be subcooled to avoid difficulties (e.g., cavitation1) in pumping. In fact, real processes will have temperature and pressure changes along the piping between individual components in the schematic, but these changes will be considered negligible in the Rankine cycle and all other processes discussed in the chapter, unless otherwise stated. These simplifications allow focus on the most important concepts, but the simplifications would be reconsidered in a detailed process design.
Leave a Reply