Let us consider how to calculate the optimum work interactions for a general system. For an open system where kinetic energy and potential energy changes are negligible,
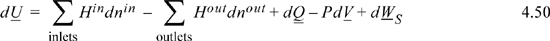
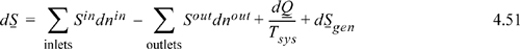
where dSgen = 0 for an internally reversible process. If all the heat is transferred at a single temperature Tsys, elimination of dQ in the first balance provides
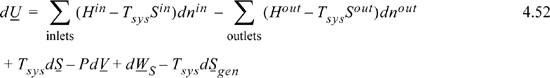
If we wish to apply this balance to a process that is conceptually reversible, we must use care to avoid any processes that are inherently irreversible (throttle valves, composition mixing processes, mixing of streams with identical composition but different temperatures, standard heat exchangers, chemical reactions at finite rates). Thus, if we consider a process that involves mixing compositions or reactions, we must include realistic estimates of these terms before determining the optimum work interaction. Once we recognize these limitations, we are ready to consider the general problem of finding optimum work interactions.
Availability (Exergy)
Section 4.5 considered optimum work interactions between a closed system and reservoir and found that optimum work interactions occur when the system temperature where heat transfer occurs is equal to the reservoir temperature. Therefore, for optimum work interactions with the surroundings, Tsys in Eqn. 4.52 should be replaced with the surrounding’s temperature To. Though it leads to optimum work, it is an idealized condition because the rate of heat transfer is proportional to the temperature difference (as studied in heat transfer courses), and the heat transfer with infinitesimal temperature differences will be infinitesimally slow. The surrounding’s temperature and pressure (To and Po) are often considered the dead state, because when the system reaches this T and P, energy input of some type is necessary to obtain expansion/contraction work, shaft work, or heat transfer; without energy input the process is dead. However, departures from this dead state do provide opportunities for work and heat interactions. Further, it is desirable to give a name to the combination of variables that results. For the combination of variables in the summations of Eqn. 4.52 modified with To, we will use the term availability, or exergy, B,
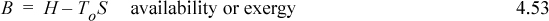
where H and S are state properties of the system at T and P, but To is the temperature of the dead state. The terms “availability” and “exergy” are both used in literature for this property. At a given T and P, the availability changes with To, so B is somewhat different from other state properties used to this point. Inserting the availability into Eqn. 4.52, and collecting the state changes of the system on the left-hand side, results in a general balance (ignoring kinetic and potential energy like before),
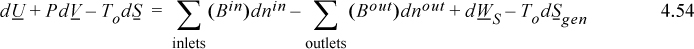
Steady-State Flow
For a system at steady-state flow, all terms on the left-hand side drop out, resulting in
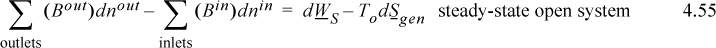
and we conclude that the difference in availability from the inlets to outlets is related to the optimum shaft work. Note that TodSgen ≥ 0 and always subtracts from work input when dWS ≥ 0 which means work input for an irreversible process is always greater than a reversible process for a given state change. Similarly, for a given state change producing work, an irreversible process will always produce less work compared to a reversible process. The quantity ToSgen is called the lost work and the reason for the term should now be obvious. To is ambiguous when no heat is transferred to the surroundings and drops out for an adiabatic process such as an adiabatic turbine without any loss in applicability of the equation,
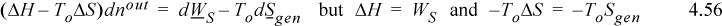
Closed System
For a closed system, Eqn. 4.54 becomes
Josiah Willard Gibbs (1839–1903) was an American chemist, mathematician, and physicist. Yale University awarded Gibbs the first American Ph.D. in Engineering in 1863 and Gibbs spent his career there. Gibbs is recognized for applying calculus to thermodynamics and combining the first and second laws. Gibbs studied the concept of chemical potential, the Gibbs phase rule, and many other relations.
For a constant-pressure closed system, VdP can be added to the left side (because it is zero in magnitude), which then results in dU + PdV + VdP = dU + d(PV) = dH. Thus, the left-hand side can be replaced with dB, though it is usually easier to calculate dH and TodS independently. We can define the Gibbs energy G ≡ H – TS. Then dG = dU + PdV + VdP – TdS – SdT. Thus, if the pressure is constant and the temperature is constant at To, then the change in Gibbs energy is related to the non-expansion/contraction work. Another interesting analysis can be done if both work terms are on the right-hand side of the equation:
Hermann Ludwig Ferdinand von Helmholtz (1821–1894) was a German physician and physicist.
Besides studying optics of the eye, he studied the concept of conservation of energy.
We can define the Helmholtz energy A ≡ U – TS. Then dA = dU – TdS – SdT. When the system is isothermal at To, then the change in Helmholtz energy is related to the sum of all forms of work.
Availability Analysis
As the world population grows and energy use increases, energy conservation will become increasingly important. Not only is the energy balance important, but so is the wise use of existing resources. Availability analysis can be used to determine how much entropy is generated by a process. Availability analysis is sometimes used in process design analysis,18 and may be used more widely in the future as we consider wise stewardship of energy resources.
Minimum Work for Separation
A key challenge in the development of a fermentation process is the titer, or yield from the fermentation. Fermentation is used in the pharmaceutical industry to develop natural molecules. For example, bacterial production of insulin is a feasible technology. Much of the cost of production depends on the dilution level. We can estimate the minimum energy cost for concentrating a product by combining the energy and entropy balances. Suppose that for a feed F we wish to obtain a pure product P and by-product water, B, in an isothermal process. For continuous separation of a mixed stream, the steady-state energy balance for a reversible separation is
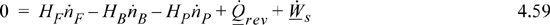
Assuming an ideal solution, we can recognize that because the heat of mixing is zero the energy balance becomes
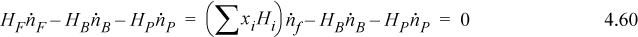
The energy balance thus simplifies to

The steady-state entropy balance for reversible separation exchanging heat at T is:
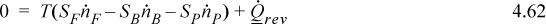
The strategy will be to determine the heat transfer from the entropy balance and then use it in the energy balance to find the work.
The entropy of the feed stream will be (using Eqn. 4.9)
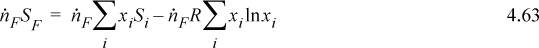
Inserting,
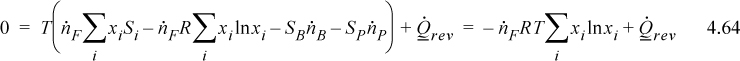
which becomes
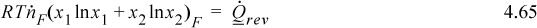
Let us suppose that component 2 is the desired species. On the basis of heat transfer per mole of component 2,
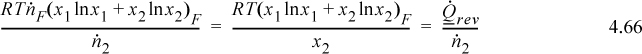
Combining with the energy balance, the minimum work per mole of desired species is
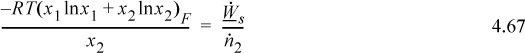
Example 4.18. Minimum heat and work of purificationa
Products produced by biological systems can range over mole fractions from 10–1 to 10–9.
a. Estimate the minimum reversible heat and work requirement to purify one mole of product at 298.15 K over this range.
b. To understand the concentrations in dilute mixtures, calculate the mole fraction of insulin in 0.1wt% aqueous solution.
Solution
The work is from Eqn. 4.67, and the heat will have the opposite sign.
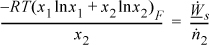
For x2 = 0.10, x1 = 0.9. At 298.15K,
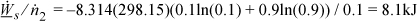
Repeating the calculation for other values of x2:.

Note that heat must be rejected. If a process is envisioned that requires heat, then the rejected heat must be increased by an equal amount. For example, if a solution of concentration x2 = 0.10 is purified by adding 1 kJ of heat, then 9.1 kJ must be rejected.
(b) Searching for the molecular weight of insulin reveals a value of 5808 g/mol. Therefore, x1 = 0.001/5808 = 1.72(10-7). The point is that biomolecules are often large, and therefore their concentrations can be quite small on a mole fraction basis.
a. This problem was suggested by O’Connell, J.P. et al. July 2010. NSF BioEMB Workshop, San Jose, CA
Leave a Reply