Before analysis involving multiple process units, it is helpful to consider the entropy balance for common steady-state process equipment. Familiarity with these common units will facilitate rapid analysis of situations with multiple units, because understanding these balances is a key step for the calculation of reversible heat and work interactions.
Simple Closed Systems
Changes in entropy affect all kinds of systems. We have previously worked with piston/cylinders and even a glass of water. You should be ready to adapt the entropy balance in creative ways to everyday occurrences as well as sophisticated equipment.
Example 4.10. Entropy generation by quenching
A carbon-steel engine casting [CP = 0.5 kJ/kg°C] weighing 100 kg and having a temperature of 700 K is heat-treated to control hardness by quenching in 300 kg of oil [CP = 2.5 kJ/kg°C] initially at 298 K. If there are no heat losses from the system, what is the change in entropy of: (a) the casting; (b) the oil; (c) both considered together; and (d) is this process reversible?
Solution
Unlike the previous examples, there are no reservoirs, and the casting and oil will both change temperature. The final temperature of the oil and the steel casting is found by an energy balance. Let Tf be the final temperature in K.
Energy balance: The total change in energy of the oil and steel is zero.
Heat lost by casting:
Q = mCpΔT = 100 (0.5) (700 – Tf)
Heat gained by oil:
Q = mCpΔT = 300 (2.5) (Tf – 298) ⇒ balancing the heat flow, Tf = 323.1 K
Entropy balance: The entropy change of the universe will be the sum of the entropy changes of the oil and casting. We will not use the entropy balance directly except to note that ΔSuniv = Sgen. We can calculate the change of entropy of the casting and oil by any reversible pathway which begins and ends at the same states. Consider an isobaric path:
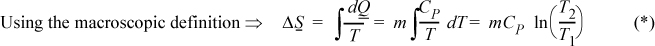
a. Change in entropy of the casting:
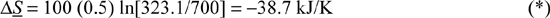
b. Change in entropy of the oil (the oil bath is of finite size and will change temperature as heat is transferred to it):
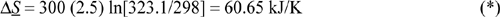
c. Total entropy change: Sgen = ΔSuniv = 60.65 – 38.7 = 21.9 kJ/K
d. Sgen > 0; therefore irreversible; compare the principles with Example 4.8 on page 152 to note the similarities. The difference is that both subsystems changed temperature.
Compare with Example 4.8 on page 152.
Heat Exchangers
The entropy balance for a standard two-stream heat exchanger is given by Eqn. 4.45. Since the unit is at steady state, the left-hand side is zero. Applying the entropy balance around the entire heat exchanger, there is no heat transfer across the system boundaries (in the absence of heat loss), so the heat-transfer term is eliminated. Since heat exchangers operate by conducting heat across tubing walls with finite temperature driving forces, we would expect the devices to be irreversible. Indeed, if the inlet and outlet states are known, the flow terms may be evaluated, thus permitting calculation of entropy generation.
We also may perform “paper” design of ideal heat transfer devices that operate reversibly. If we set the entropy generation term equal to zero, we find that the inlet and outlet states are constrained. Since there are multiple streams, the temperature changes of the streams are coupled to satisfy the entropy balance. In order to construct such a reversible heat transfer device, the unit would need to be impracticably large to only have small temperature gradients.
Example 4.11. Entropy in a heat exchanger
A heat exchanger for cooling a hot hydrocarbon liquid uses 10 kg/min of cooling H2O which enters the exchanger at 25°C. Five kg/min of hot oil enters at 300°C and leaves at 150°C and has an average specific heat of 2.51 kJ/kg-K.
a. Demonstrate that the process is irreversible as it operates now.
b. Assuming no heat losses from the unit, calculate the maximum work which could be obtained if we replaced the heat exchanger with a Carnot device which eliminates the water stream and transfers heat to the surroundings at 25°C
Solution
a. System is heat exchanger (open system in steady-state flow)
Energy balance:
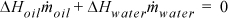
10(4.184)(Twout – 25) + 5(2.51)(150 – 300) = 0; Twout = 70°C
Entropy balance:
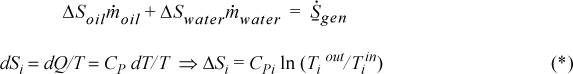
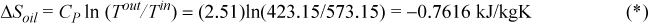
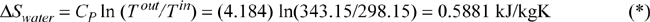
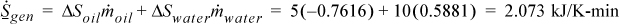
The process is irreversible because entropy is generated.
b. The modified process is represented by the “device” shown below. Note that we avoid calling the device a “heat exchanger” to avoid confusion with the conventional heat exchanger. To simplify analysis, the overall system boundary is used.
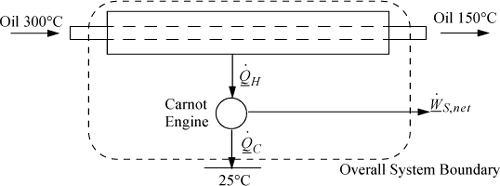
By an energy balance around the overall system, 
. We can only solve for the enthalpy term,
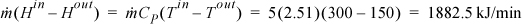
Since heat and work are both unknown, we need another equation. Consider the entropy balance, which, since it is a reversible process, 
, gives
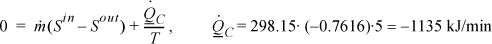
Now inserting these results into the overall energy balance gives the work,
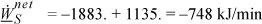
Throttle Valves
Steady-state throttle valves are typically assumed to be adiabatic, but a finite pressure drop with zero recovery of work or kinetic energy indicates that 
. Throttles are isenthalpic, and for an ideal gas, they are thus isothermal, 
. For a real fluid, temperature changes can be significant. The entropy increase is large for gases, and small, but nonzero for liquids. It is important to recall that liquid streams near saturation may flash as they pass through throttle valves, which also produces large entropy changes and significant cooling of the process fluid even when the process is isenthalpic. Throttles involving flash are common in the liquefaction and refrigeration processes discussed in the next chapter. Throttles are always irreversible.
Nozzles
Steady-state nozzles can be designed to operate nearly reversibly; therefore, we may assume 
, and Eqn. 4.47 applies. Under these conditions, thrust is maximized as enthalpy is converted into kinetic energy. The distinction between a nozzle and a throttle is based on the reversibility of the expansion. Recall from Chapter 2 that a nozzle is specially designed with a special taper to avoid turbulence and irreversibilities. Naturally, any real nozzle will approximate a reversible one and a poorly designed nozzle may operate more like a throttle. Proper design of nozzles is a matter of fluid mechanics. We can illustrate the basic thermodynamic concepts of a properly designed nozzle with an example.
Example 4.12. Isentropic expansion in a nozzle
Steam at 1000°C and 1.1 bars passes through a horizontal adiabatic converging nozzle, dropping to 1 bar. Estimate the temperature, velocity, and kinetic energy of the steam at the outlet assuming the nozzle is reversible and the steam can be modeled with the ideal gas law under the conditions. Consider the initial velocity to be negligible. The highest exit velocity possible in a converging nozzle is the speed of sound. Use the NIST web sitea as a resource for the speed of sound in steam at the exit conditions.
Solution
For an isentropic reversible expansion the temperature will drop. We will approximate the heat capacity with an average value. Let us initially use a CP for 650 K. Estimating the heat capacity from Appendix E at 650 K, the polynomial gives CP = 44.6 J/mol, R/CP ~ 8.314/44.6 = 0.186. The following relation satisfies the entropy balance for an adiabatic, reversible, ideal gas (Eqn. 4.29):
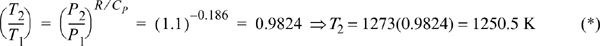
The temperature change is small, so the constant heat capacity assumption is fine. The enthalpy change is –ΔH = –CPΔT = 44.6(1273 – 1250.5)(J/mol) = 1004 J/mol.
Assuming that the inlet velocity is low, v1 ~ 0 and converting the enthalpy change to the change in velocity gives v2 = –2ΔH/m = 2·1004J/mol(mol/18.01g)(1000g/kg)(1kg-m2/s2)/J = 111,500 m2/s2, or v = 334 m/s. According to the NIST web site at 1250K and 0.1MPa, the speed of sound is 843 m/s. The design is reasonable.
a. Lemmon, E.W., McLinden, M.O., Friend, D.G. “Thermophysical Properties of Fluid Systems.” in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, P.J. Linstrom, W.G. Mallard (eds.) National Institute of Standards and Technology, Gaithersburg, MD. http://webbook.nist.gov, (retrieved November 12, 2011).
Adiabatic Turbine, Compressor, and Pump
The entropy balance for a steady-state adiabatic device is:
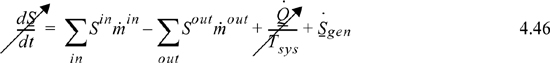
The left-hand side drops out because the system is at steady state. If the device is reversible, 
is zero. Further, these devices typically have a single inlet or outlet,17 and 
, thus,
Adiabatic reversible turbine, compressor, and pump.
Therefore, if we know the inlet state, we can find Sin. The outlet pressure is generally given, so for a pure fluid, the outlet state is completely specified by the two state variables Sout and Pout. We then use thermodynamic relations to find the other thermodynamic variables at this state, and use the energy balance at this state to find Wrev. Turbines, compressors, and pumps are very common equipment in chemical processes. Guidelines exist for estimating the degree of irreversibility in each piece of equipment based on experience. These guidelines take the form of an estimated efficiency. For example, a large expensive turbine might be 85% efficient, but a small cheap one might be 65% efficient. To apply these guidelines, we must formally define efficiency, then familiarize ourselves with variations on how to characterize the capacity and operating conditions of these operations.
Leave a Reply