In the introduction to this chapter, we alluded to the relation between entropy and maximum process efficiency. We have shown that entropy changes with volume (pressure) and temperature. How can we use entropy to help us determine maximum work output or minimum work input? The answer is best summarized by a series of statements. These statements refer to the entropy of the universe. This does not mean that we imagine measuring entropy all over the universe. It simply means that entropy may decrease in one part of a system but then it must increase at least as much in another part of a system. In assessing the reversibility of the overall system, we must sum all changes for each process in the overall system and its surroundings. This is the relevant part of the universe for our purposes.
Molar or specific entropy is a state property which will assist us in the following ways.
1. Irreversible processes will result in an increase in entropy of the universe. (Irreversible processes will result in entropy generation.) Irreversible processes result in loss of capability for performing work.
2. Reversible processes result in no increase in entropy of the universe. (Reversible processes result in zero entropy generation. This principle will be useful for calculation of maximum work output or minimum work input for a process.)
3. Proposed processes which would result in a decrease of entropy of the universe are impossible. (Impossible processes result in negative entropy generation.)
These three principles are summarized in the second law of thermodynamics: Reversible processes and/or optimum work interactions occur without entropy generation, and irreversible processes result in entropy generation. The microscopic descriptions in the previous section teach us very effectively about the relation between entropy and disorder, but it is not fair to say that any increase in volume results in a loss of potentially useful work when the entropy of the system increases. (Note that it is the entropy change of the universe that determines irreversibility, not the entropy change of the system.) After all, the only way of obtaining any expansion/contraction work is by a change in volume. To understand the relation between lost work and volume change, we must appreciate the meaning of reversibility, and what types of phenomena are associated with entropy generation. We will explore these concepts in the next sections.
The entropy balance is the second law of thermodynamics.
Entropy Definition (Macroscopic)
Let us define the differential change in entropy of a closed simple system by the following equation:
For a change in states, both sides of Eqn. 4.12 may be integrated,
where the following occurs:
1. The entropy change on the left-hand side of Eqn. 4.13 is dependent only on states 1 and 2 and not dependent on reversibility. However, to calculate the entropy change via the integral, the integral may be evaluated along any convenient reversible pathway between the actual states.
2. Tsys is the temperature of the system boundary where heat is transferred. Only if the system boundary temperature is constant along the pathway may this term be taken out of the integral sign.
A change in entropy is completely characterized for a pure single-phase fluid by any other two state variables. It may be surprising that the integral is independent of the path since Q is a path-dependent property. The key is to understand that the right-hand side integral is independent of the path, as long as the path is reversible. Thus, a process between two states does not need to be reversible to permit calculation of the entropy change, since we can evaluate it along any reversible path of choice. If the actual path is reversible, then the actual heat transfer and pathway may be used. If the process is irreversible, then any reversible path may be constructed for the calculation.
Entropy is a state property. For a pure single-phase fluid, specific entropy is characterized by two state variables (e.g., T and P).
Look back at Example 4.1 and note that the entropy change for the isothermal process was calculated by the microscopic formula. However, look at the process again from the perspective of Eqn. 4.13 and subsequent statement 2. Because the process was isothermal, the entropy change can be calculated ΔS = Qrev/Tsys; try it! Note that the irreversible process in that example exhibits the same entropy change, calculated by the reversible pathway.
Now, look back at the integral of Eqn. 4.13 and consider an adiabatic, reversible process; the process will be isentropic (constant entropy, ΔS = 0). Let us consider how the entropy can be used as a state property to identify the final state along a reversible adiabatic process. Further, the property does not depend on the limitations of the ideal gas law. The ideal gas law was convenient to introduce the property. Consider the adiabatic reversible expansion of steam, a non-ideal gas. We can read S values from the steam tables.
Example 4.3. Adiabatic, reversible expansion of steam
Steam is held at 450°C and 4.5 MPa in a piston/cylinder. The piston is adiabatically and reversibly expanded to 2.0 MPa. What is the final temperature? How much reversible work can be done?
Solution
The T, P are known in the initial state, and the value of S can be found in the steam tables. Steam is not an ideal gas, but by Eqn. 4.12, the process is isentropic because it is reversible and adiabatic. From the steam tables, the entropy at the initial state is 6.877 kJ/kgK. At 2 MPa, this entropy will be found between 300°C and 350°C. Interpolating,
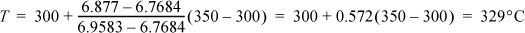
The P and Sf = Si are known in the final state and these two state properties can be used to find all the other final state properties. The work is determined by the energy balance: ΔU = Q + WEC. The initial value of U is 3005.8 kJ/kg. For the final state, interpolating U by using Sf at Pf, U = 2773.2 + 0.572(2860.5 – 2773.2) = 2823.1 kJ/kg, so
WEC = (2823.1 – 3005.8) = –182.7 kJ/kg
Let us revisit the Carnot cycle of Section 3.1 in light of this new state property, entropy. The Carnot cycle was developed with an ideal gas, but it is possible to prove that the cycle depends only on the combination of two isothermal steps and two adiabatic steps, not the ideal gas as the working fluid.14 Because the process is cyclic, the final state and initial state are identical, so the overall entropy changes of the four steps must sum to zero, ΔS = 0. Because the reversible, adiabatic steps are isentropic, ΔS = 0, the entropy change for the two isothermal steps must sum to zero. As we discussed above, for an isothermal step Eqn. 4.13 becomes ΔS = Qrev/T. Therefore, an analysis of the Carnot cycle from the viewpoint of entropy is
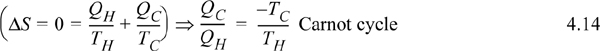
This can be inserted into the formula for Carnot efficiency, Eqn. 3.6. Note that this relation is not constrained to an ideal gas! In fact, there are only three constraints for this balance: The process is cyclic; all heat is absorbed at TH; all heat is rejected at TC. Example 4.4 shows how the Carnot cycle can be performed with steam including phase transformations.
Example 4.4. A Carnot cycle based on steam
Fig. 4.3 shows the path of a Carnot cycle operating on steam in a continuous cycle that parallel the two isothermal steps and two adiabatic steps of Section 3.1. First, saturated liquid at 5 MPa is boiled isothermally to saturated vapor in step (a→b). In step (b→c), steam is adiabatically and reversibly expanded from saturated vapor at 5 MPa to 1 MPa. In (c→d), heat is isothermally removed and the volume drops during condensation. Finally, in step (d→a), the steam is adiabatically and reversibly compressed to 5 MPa and saturated liquid. (Hint: Challenge yourself to solve the cycle without looking at the solution.).
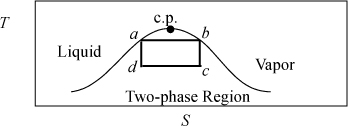
Figure 4.3. A T-S diagram illustrating a Carnot cycle based on steam.
a. Compute W(a→b) and QH.
b. Compute W(b→c).
c. Compute W(d→a). (The last step in the cycle).
d. Compute W(c→d) and QC. (The third step in the cycle).
e. For the cycle, compute the thermal efficiency by ηθ = –Wnet/QH and compare to Carnot’s efficiency, ηθ = (TH – TL)/TH.
Solution
The entropy change is zero for the expansion and compression steps because these steps are adiabatic and reversible, as indicated by the vertical line segments in Fig. 4.3.
a. E-balance: fixed P,T vaporization, QH = ΔU – WEC = (ΔU + PΔV) = ΔHvap = 1639.57 J/kg; WEC(a→b) = PΔV = 5(0.0394 – 0.001186)*1000 = 191.1 J/kg.
b. E-balance: isentropic, WEC(b→c) = ΔU; Ub = U(sat. vap., 5MPa) = 2596.98 kJ/kg; S-balance: ΔS = 0; Sc = Sb = 5.9737 kJ/kg-K= qc(6.5850) + (1 – qc)2.1381; qc = 0.8625; Uc = 0.8625(2582.75) + (1 – 0.8625)761.39 = 2332.31 kJ/kg; WEC(b→c) = 2332.31 – 2596.98 = –264.67 kJ/kg.
c. This is the last step. E-balance: isentropic. WEC(d→a) = ΔU; Ud = U(sat. liq., 5MPa) = 1148.21 kJ/kg; the quality at state d is not known, but we can use the entropy at state a to find it. S-balance: ΔS = 0; Sd = Sa = 2.9210 kJ/kg-K= qd(6.5850) + (1 – qd)2.1381; qd = 0.1761; Ud = 0.1761(2582.75) + (1 – 0.1761)761.39 = 1082.13 kJ/kg; WEC(d→a) = 1082.13 – 1148.21 = –66.08 kJ/kg.
d. This is the third step using the quality for d calculated in part (c). This is a fixed T,P condensation. E-balance: QC = ΔU – WEC = (ΔU+PΔV) = ΔH; Hd = 762.52 + 0.1761(2014.59) = 1117.29 kJ/kg; Hc= 762.52 + 0.8625(2014.59) = 2500.10 kJ/kg; QC = Hd – Hc = –1382.21 kJ/kg WEC = PΔV; Vc = 0.001127(1 – 0.8625) + 0.8625(0.1944) = 0.1678 m3/kg = 167.8 cm3/g Vd = 0.001127(1 – 0.1761)+0.1761(0.1944) = 0.0352 m3/kg = 35.2 cm3/g W(c→d) = 1.0(35.2 – 167.8) = –132.6 MPa-cm3/g = –132.6 kJ/kg
e. ηθ = –Wnet/QH; Wnet = (264.67–66.08+191.1–132.6) = 257.1 kJ/kg; ηθ = 257.1/1639.57 = 0.157; ηθ (Carnot) = (263.94–179.88)/(263.94+273.15) = 0.157. The actual cycle matches the Carnot formula. Note that the cyclic nature of this process means that we could have computed more quickly by Wnet = –(QC + QH) = 1382.21 – 1639.57 = 257.4 kJ/kg.
The macroscopic view of entropy can be bewildering when first studied because students strive to understand the physical connection. The microscopic view of entropy is helpful for some students but a significant disconnect often persists. In either case, if you review the definitions at the beginning of the chapter, both are mathematical, not physical. In Chapter 2 we discussed that Q was a path-dependent property, but now we are demonstrating that dividing the quantity by T and integrating along a path results in a quantity that is independent of the path!15 Some students find it helpful to accept this as a mathematical relationship with the name of “entropy.” In fact, development of the macroscopic definition of entropy was not obvious to the scientists who eventually proved it to be a state property. The scientific literature at the time of Carnot can be confusing to read because the realization of the state nature of the integral was not obvious, but was developed by a significant amount of diligence and insight by the scientists of the day.
Entropy can be used to decouple heat and work.
Note that entropy does not depend directly on the work done on a system. Therefore, it may be used to decouple heat and work in the energy balance for reversible processes. Also for reversible processes, entropy provides a second property that may be used to determine unknowns in a process as we have seen in the previous two examples. In fact, the power of this property is that it can be used to evaluate reversibility of processes, and such understanding is critical as we search sustainable energy management practices, such as CO2 sequestration. Let us investigate some convenient pathways for the evaluation of entropy changes before we develop examples that utilize the pathways.
Calculation of Entropy Changes in Closed Systems
As with enthalpy and internal energy, tables and charts are useful sources for entropy information for common fluids. Note the tabulation of S in the tables of Appendix E. These tables and charts are calculated using the definition of entropy and procedures for non-ideal fluids that we will discuss in upcoming chapters.
For manual calculations of entropy, we develop some simple procedures here, and more rigorous procedures in Chapter 8. Since the integral of Eqn. 4.13 must be evaluated along a reversible path, let us consider some easy choices for paths. For a closed reversible system without shaft work, the energy balance in Eqn. 2.16 becomes,
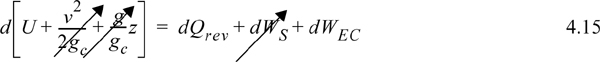
Inserting Eqn. 2.3,
We now consider how this equation may be substituted in the integral of Eqn. 4.13 for calculating entropy changes in several situations.
Constant Pressure (Isobaric) Pathway
Many process calculations involve state changes at constant pressure. Recognizing H = U + PV, dH = dU + PdV + VdP. In the case at hand, dP happens to be zero; therefore, Eqn. 4.16 becomes
Since dH = CPdT at constant pressure, along a constant-pressure pathway, substituting for dQrev in Eqn. 4.13, the entropy change is
Constant Volume Pathway
For a constant volume pathway, Eqn. 4.16 becomes
Since dU = CVdT along a constant volume pathway, substituting for dQrev in Eqn. 4.13, the entropy change is
Constant Temperature (Isothermal) Pathway
The behavior of entropy at constant temperature is more difficult to generalize in the absence of charts and tables because dQrev depends on the state of aggregation. For the ideal gas, dU = 0 = dQ – PdV, dQ = RTdV/V, and plugging into Eqn. 4.13,
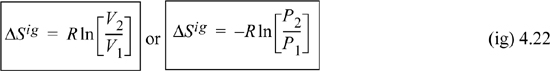
For a liquid or solid, the effect of isothermal pressure of volume change is small as a first approximation; the precise relations for detailed calculations will be developed in Chapters 6–8. Looking at the steam tables at constant temperature, entropy is very weakly dependent on pressure for liquid water. This result may be generalized to other liquids below Tr = 0.75 and also to solids. For condensed phases, to a first approximation, entropy can be assumed to be independent of pressure (or volume) at fixed temperature.
Adiabatic Pathway
A process that is adiabatic and reversible will result in an isentropic path. By Eqn. 4.13,
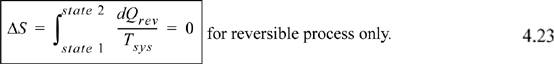
Note that a path that is adiabatic, but not reversible, will not be isentropic. This is because a reversible adiabatic process starting at the same state 1 will not follow the same path, so it will not end at state 2, and reversible heat transfer will be necessary to reach state 2.
Phase Transitions
In the absence of property charts or tables, entropy changes due to phase transitions can be easily calculated. Since equilibrium phase transitions for pure substances occur at constant temperature and pressure, for vaporization
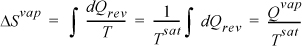
where Tsat is the equilibrium saturation temperature. Likewise for a solid-liquid transition,
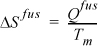
where Tm is the equilibrium melting temperature. Since either transition occurs at constant pressure if along a reversible pathway, we may include Eqn. 4.17, giving
Now let us examine a process from Chapter 2 that was reversible, and study the entropy change. We will show that the result is the same via two different paths, confirming that entropy is a state function.
Example 4.5. Ideal gas entropy changes in an adiabatic, reversible expansion
In Example 2.11 on page 75, we derived the temperature change for a closed-system adiabatic expansion of an ideal gas. How does the entropy change along this pathway, and what does this example show about changes in entropy with respect to temperature?
Solution
Reexamine the equation (CV/T)dT = –(R/V)dV, which may also be written (CV/R)dln T = –dIn V. We can sketch this path as shown by the diagonal line in Fig. 4.4. Since our path is adiabatic (dQ = 0) and reversible, and our definition of entropy is dS = (dQrev)/T, we expect that this implies that the path is also isentropic (a constant-entropy path). Since entropy is a state property, we can verify this by calculating entropy along the other pathway of the figure consisting of a constant temperature (step A) and a constant volume (step B)
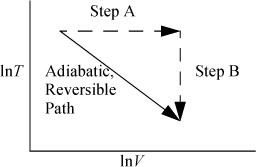
Figure 4.4. Equivalence of an adiabatic and an alternate path on a T-V diagram.
For the reversible isothermal step we have
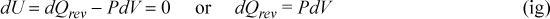
Thus,
Substituting the ideal gas law,
For the constant volume step, we have
dU = dQrev or CVdT = dQrev
Thus,
We could replace a differential step along the adiabat (adiabatic pathway) with the equivalent differential steps along the alternate pathways; therefore, we can see that the change in entropy is zero,
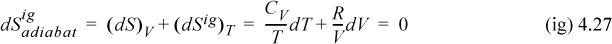
which was shown by the energy balance in Eqn. 2.62, and we verify that the overall expansion is isentropic. Trials with additional pathways would show that ΔS is the same.
The entropy change along the adiabatic, reversible path is the same as along (step A + step B) illustrating that S is a state property.
The method of subdividing state changes into individual temperature and volume changes can be generalized to any process, not just the adiabatic process of the previous example, giving
We may integrate steps A and B independently. We also could use temperature and pressure steps to calculate entropy changes, resulting in an alternate formula:
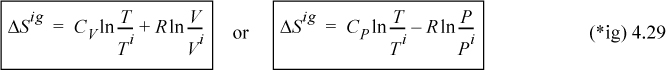
As an exercise, you may wish to choose two states and find the change in S along two different pathways: first with a step in T and then in P, and then by inverting the steps. The heat and work will be different along the two paths, but the change in entropy will be the same.
Looking back at Eqn. 4.26, we realize that it does not depend on the ideal gas assumption, and it is a general result,
Temperature derivatives of entropy are related to CP and CV.
which provides a relationship between CV and entropy. Similarly, looking back at Eqn. 4.18,
Eqns. 4.30 and 4.31 are particularly easy to apply for ideal gases. In fact, the most common method for evaluating entropy changes with temperature applies Eqn. 4.31 in this way, as shown below.
Example 4.6. Ideal gas entropy change: Integrating CPig(T)
Propane gas undergoes a change of state from an initial condition of 5 bar and 105°C to 25 bar and 190°C. Compute the change in enthalpy using the ideal gas law.
Solution
Because P and T are specified in each state, the ideal gas change is calculated most easily by combining an isobaric temperature step, Eqns. 4.19, and an isothermal pressure change, Eqn. 4.22. The heat capacity constants are obtained from Appendix E.
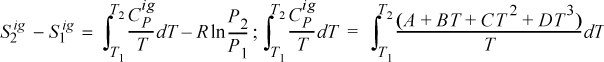
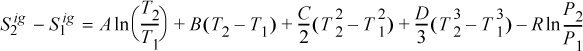
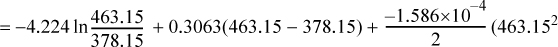
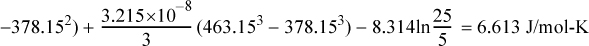
Entropy Generation
At the beginning of Section 4.3 on page 142, statement number one declares that irreversible processes generate entropy. Now that some methods for calculating entropy have been presented, this principle can be explored.
Example 4.7. Entropy generation and “lost work”
In Example 4.1 consider the surroundings at 300 K: (a) Consider the entropy change in the surroundings and the universe for parts 4.1(a) and 4.1(b) and comment on the connection between entropy generation and lost work; (b) How would entropy generation be affected if the surroundings are at 310 K?
Solution
a. For 4.1(a) the entropy change of the surroundings is 
. This is equal and opposite to the entropy change of the piston/cylinder, so the overall entropy change is ΔSuniverse = 0.
For part 4.1(b), the entropy change of the universe is ΔSsurr = Q/300 = –1995/300 = –6.65J/K. The total entropy change is ΔSuniverse = 13.38–6.65 = 6.73J/K > 0, thus entropy is generated when work is lost.
b. If the temperature of the surroundings is raised to 310K, then for the reversible piston cylinder expansion for 4.1(a), ΔSsurr = –4014/310 = –12.948J/K, and ΔSuniverse = 13.38 – 12.95 = 0.43J/K > 0. This process now will have some ‘lost work’ due to the temperature difference at the boundary even though the piston/cylinder and work was frictionless without other losses. We will reexamine heat transfer in a gradient in a later example. For case 4.1(b), the entropy generation is still greater, indicating more lost work, ΔSsurr = –1995/310 = –6.43J/K, ΔSuniverse = 13.38 – 6.43 = 6.95J/K > 0.
This is an irreversible process because entropy is generated.
Note: When the entropy change for the universe is positive the process is irreversible. Because entropy is a state property, the integrals that we calculate may be along any reversible pathway, and the time dependence along that pathway is unimportant.
We discussed in Chapter 2 that friction and velocity gradients result in irreversibilities and thus entropy generation occurs. Entropy generation can also occur during heat transfer, so let us consider that possibility.
Example 4.8. Entropy generation in a temperature gradient
A 500 mL glass of chilled water at 283 K is removed from a refrigerator. It slowly equilibrates to room temperature at 298 K. The process occurs at 1 bar. Calculate the entropy change of the water, ΔSwater, the entropy change of the surroundings, ΔSsurr, and the entropy change of the universe, ΔSuniv. Neglect the heat capacity of the container. For liquid water CP = 4.184 J/g-K.
Solution
Water: The system is closed at constant pressure with Ti = 283 K and Tf = 298 K. We choose any reversible pathway along which to evaluate Eqn. 4.13, a convenient path being constant-pressure heating. Thus,
dQrev = dH = mCPdT
Substituting this into our definition for a change in entropy, and assuming a T-independent CP,
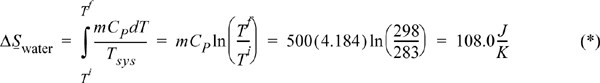
Surroundings: The surroundings also undergo a constant pressure process as a closed system; however, the heat transfer from the glass causes no change in temperature—the surroundings act as a reservoir and the temperature is 298 K throughout the process. The heat transfer of the surroundings is the negative of the heat transfer of the water, so we have
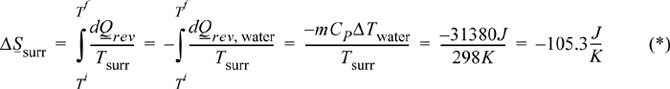
Note that the temperature of the surroundings was constant, which simplified the integration.
Universe: For the universe we sum the entropy changes of the two subsystems that we have defined. Summing the entropy change for the water and the surroundings we have
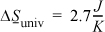
Entropy has been generated. The process is irreversible.
Leave a Reply