3.1. Two moles of nitrogen are initially at 10 bar and 600 K (state 1) in a horizontal piston/cylinder device. They are expanded adiabatically to 1 bar (state 2). They are then heated at constant volume to 600 K (state 3). Finally, they are isothermally returned to state 1. Assume that N2 is an ideal gas with a constant heat capacity as given on the back flap of the book. Neglect the heat capacity of the piston/cylinder device. Suppose that heat can be supplied or rejected as illustrated below. Assume each step of the process is reversible.
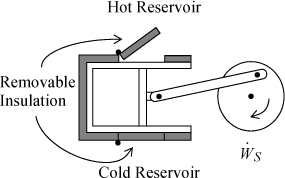
a. Calculate the heat transfer and work done on the gas for each step and overall.
b. Taking state 1 as the reference state, and setting 
, calculate U and H for the nitrogen at each state, and ΔU and ΔH for each step and the overall Q and WEC.
c. The atmosphere is at 1 bar and 298 K throughout the process. Calculate the work done on the atmosphere for each step and overall. (Hint: Take the atmosphere as the system.) How much work is transferred to the shaft in each step and overall?
3.2. One mole of methane gas held within a piston/cylinder, at an initial condition of 600 K and 5 MPa, undergoes the following reversible steps. Use a temperature-independent heat capacity of CP = 44 J/mol-K.
a. Step 1: The gas is expanded isothermally to 0.2 MPa, absorbing a quantity of heat QH1. Step 2: The gas is cooled at constant volume to 300 K. Step 3. The gas is compressed isothermally to the initial volume. Step 4: The gas is heated to the initial state at constant volume requiring heat transfer QH2. Calculate ΔU, Q, and WEC for each step and for the cycle. Also calculate the thermal efficiency that is the ratio of total work obtained to heat furnished, 
.
b. Step 1: The gas is expanded to 3.92 MPa isothermally, absorbing a quantity of heat QH1. Step 2: The gas is expanded adiabatically to 0.1 MPa. Step 3: The gas is compressed isothermally to 0.128 MPa. Step 4: The gas is compressed adiabatically to the initial state. Calculate ΔU, Q, WEC for each step and for the cycle. Also calculate the thermal efficiency for the cycle, 
.
3.3. The Arrhenius model of global warming constitutes a very large composite system.3 It assumes that a layer of gases in the atmosphere (A) absorbs infrared radiation from the Earth’s surface and re-emits it, with equal amounts going off into space or back to the Earth’s surface; 240 W/m2 of the solar energy reaching the Earth’s surface is reflected back as infrared radiation (S). The “emissivity value” (λ) of the ground (G) is set equal to that of A. λ characterizes the fraction of radiation that is not absorbed. For example, (1–λ) would be the fraction of IR radiation that is absorbed by the ground, and the surface energy would be S = Aλ + G(1–λ). A similar balance for the atmosphere gives, λG = 2λA. This balance indicates that radiation received from G is balanced by that radiated from A. The factor of 2 on the right-hand side appears because radiation can be toward the ground or toward space. The equations for radiation are given by the relations: G = σTG4 and A = σTA4 where σ = Stefan-Boltzmann constant 5.6704 x 10-8 (W/m2-K4).
a. Noting that the average TG is 300 K, solve for λ.
b. Solve for TG when λ = 0. This corresponds to zero global warming.
c. Solve for TG when λ = 1. This corresponds to perfect global warming.
d. List at least three oversimplifications in the assumptions of this model. Discuss whether these lead to underestimating or overestimating TG.
3.4. A distillation column with a total condenser is shown in Fig. 3.3. The system to be studied in this problem has an average enthalpy of vaporization of 32 kJ/mol, an average 
of 146 J/mol°-C, and an average 
of 93 J/mol°-C. Variable names for the various stream flow rates and the heat flow rates are given in the diagram. The feed can be liquid, vapor, or a mixture represented using subscripts to indicate the vapor and liquid flows, F = FV + FL. The enthalpy flow due to feed can be represented as: for saturated liquid, FLHsatL; for saturated vapor, FVHsatV; for subcooled liquid, FLHsatL + FLCPL(TF – TsatL); for superheated vapor, FVHsatV + FVCPV(TF – TsatV); and for a mix of vapor and liquid, FLHsatL + FVHsatV.
a. Use a mass balance to show FV + VS – VR = LS – LR – FL.
[For parts (b)–(f), use the feed section mass and energy balances to show the desired result.]
b. For saturated vapor feed, FL = 0. Show VR = VS + FV, LS = LR.
c. For saturated liquid feed, FV = 0. Show VS = VR, LS = LR + FL.
d. For subcooled liquid feed, FV = 0. Show VR – VS = FLCP(TF – Tsat)/ΔHvap.
e. For superheated vapor feed, FL = 0. Show LS – LR = –FVCP(TF – Tsat)/ΔHvap.
f. For a feed mixture of saturated liquid and saturated vapor. Show VR = VS + FV, LS = LR + FL.
g. Use the mass and energy balances around the total condenser to relate the condenser duty to the enthalpy of vaporization, for the case of streams LR and D being saturated liquid.
h. Use the mass and energy balances around the reboiler to relate the reboiler duty to the enthalpy of vaporization.
i. In the case of subcooled liquid streams LR and D, the vapor flows out of the top of the column, and more variables are required. 
(into the condenser) will be smaller than the rectifying section flow rate VR. Also, the liquid flow rate in the rectifying section, LR, will be larger than the reflux back to the column, 
. Using the variables , to represent the flow rate out of the top of the column and the reflux, respectively, relate VR to , and the degree of subcooling TL′, – TsatL.
[For parts (j)–(o), find all other flow rates and heat exchanger duties (Q values).]
j. F = 100 mol/hr (saturated vapor), B = 43, LR/D = 2.23.
k. F = 100 mol/hr (saturated vapor), D = 48, LS/VS = 2.5.
l. F = 100 mol/hr (saturated liquid), D = 53, LR/D = 2.5.
m. F = 100 mol/hr (half vapor, half liquid), B = 45, LS/VS = 1.5.
n. F = 100 mol/hr (60°C subcooled liquid), D = 53, LR/D = 2.5.
o. F = 100 mol/hr (60°C superheated vapor), D = 48, LS/VS = 1.5.
3.5. Allyl chloride (AC) synthesis provides a simple prototype of many petrochemical processes. 869 kg per hour of propylene (C3) are fed with a 1% excess of chlorine (Cl2) at 25°C. The entire process operates at roughly 10 bar. Cl2 is recycled to achieve a 50% excess of Cl2 at the reactor inlet. The reactor conversion is 100% of the propylene to AC and hydrochloric acid (HCl) at 511°C.
The reactor effluent is cooled to 35°C and sent to a distillation column where 98% of the entering AC exits the bottom with 1% of the entering Cl2 and no HCl. This AC product stream exits at 57°C. The tops of the first column are sent to a second column where 99% of the entering Cl2 exits the bottom at 36°C, along with 1% of the entering HCl, all of the AC, and is recycled. The tops of the second column exit at -31°C and are sent for waste treatment. Using the method of Heat of Formation method for the energy balance and ideal gas reference states with Eqn. 2.45 to estimate the heat of vaporization, complete the following.
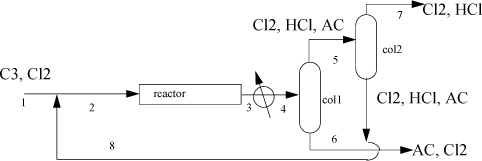
a. Write a balanced stoichiometric equation for this reaction. (Hint: Check the NIST WebBook for chemical names and formulas.)
b. Perform a material balance to determine compositions and flow rates for all streams.
c. Using only streams (1), (6), (7), calculate the energy balance in MJ/h of the entire process. Does the process involve a net energy need or surplus?
d. Determine the heat load on the reactor in MJ/h.
e. Calculate the enthalpies in MJ/h of the feed stream 1.
f. Calculate the enthalpy in MJ/h of the stream 4 entering the first distillation column.
g. Calculate the enthalpy in MJ/h of the AC product stream 6.
h. Calculate the enthalpy in MJ/h of the Cl2 recycle stream 8.
i. Calculate the enthalpy in MJ/h of the HCl waste stream 7.
3.6. Chlorobenzene(l) is produced by reacting benzene(l) initially at 30°C with Cl2(g) initially at 30°C in a batch reactor using AlCl3 as a catalyst. HCl(g) is a by-product. During the course of the reaction, the temperature increases to 50°C. To avoid dichlorobenzenes, conversion of benzene is limited to 30%. On the basis of 1 mol of benzene, and 0.5 mol Cl2(g) feed, what heating or cooling is required using the specified method(s)? The NIST WebBook reports the heats of formation for liquid benzene and chlorobenzene at 25°C as 49 kJ/mol and 11.5 kJ/mol, respectively. The heat capacities of liquid benzene and chlorobenzene are 136 J/mol-K and 150 J/mol-K, respectively.
a. Use liquid reference states for the benzenes and the heat of reaction method for the energy balance.
b. Follow part (a), but instead, use the heat of formation method for the energy balance.
c. Use an ideal gas-phase reference state for the benzenes, Eqn. 2.45 to estimate the heat of vaporization, and the Heat of Reaction method.
3.7. Benzene and benzyl chloride produced from the reaction described in problem 3.6 are separated by distillation at 1 bar. The chlorine and HCl are removed easily and this problem concerns only a binary mixture. Suppose the liquid flow to the reboiler is 90 mol% chlorobenzene and 10 mol% benzene at 121.9°C. The boilup ratio is 0.7 at 127.8°C, and the vapor leaving the reboiler is 12.7 mol% benzene. The heat of vaporization of chlorobenzene is 41 kJ/mol. Heat capacities for liquids are in problem 3.6(a). Determine the heat duty for the reboiler.
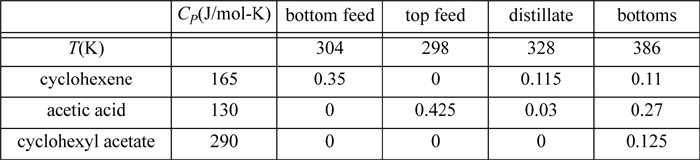
3.8. In the process of reactive distillation, a reaction occurs in a distillation column simultaneously with distillation, offering process intensification. Consider a reactive distillation including the reaction: cyclohexene(l) + acetic acid(l) 
cyclohexyl acetate(l). In a reactive distillation two feeds are used, one for each reactant. In a small-scale column, the flows, heat capacities, and temperatures are tabulated below in mol/min. Assume the heat capacities are temperature-independent. All streams are liquids. Use data from the NIST WebBook for heats of formation to estimate the net heat requirement for the column.
3.9. This problem considers oxidation of glucose as a model carbohydrate.
a. In the human body glucose is typically metabolized in aqueous solution. Ignoring the enthalpy change due to dissolving glucose in the aqueous solution, calculate the standard heat of reaction for Eqn. 3.56.
b. Using the standard heat of reaction calculated in part (a) together with the steady-state energy expenditure for sitting at rest, determine the rate that glucose is consumed (g/day). You may ignore sensible heats because the respiration streams are very close to 298.15 K.
c. Compare the energy consumption in part (b) with a light bulb by putting the energy consumption in terms of W, which is usually used to characterize light bulbs. How many 70 kg humans collectively produce energy equivalent to a 1500 W hair dryer?
d. On a mass basis, all carbohydrates have about the same heat of reaction. A soft drink has approximately 73 g carbohydrates (sugar) per 20 fluid oz. bottle and the manufacturer’s label reports that the contents provide 275 kcal. (Note: A dietary calorie is a thermodynamic kcal, so the conversion has already been made, and the bottle is labeled 275 calories.) Convert the answer from part (a) to kcal/g and compare with the manufacturer’s ratio.
e. What is the annual output of CO2 (kg) for a 70 kg human using the energy expenditure for sitting as an average value?
3.10. Compressed air at room temperature (295 K) is contained in a 20-L tank at 2 bar. The valve is opened and the tank pressure falls slowly and isothermally to 1.5 bar. The frictionless piston-cylinder is isothermal and isobaric (P = 1.5 bar) during the movement. The surroundings are at 1 bar. The volumes of the piping and valve are negligible. During the expansion, the piston is pushing on external equipment and doing useful work such that the total resistance to the expansion is equivalent to 1.5 bar. The entire system is then cooled until all of the air is back in the original container. During the retraction of the piston, the piston must pull on the equipment, and the resistance of the external equipment is equivalent to 0.1 bar, so the total force on the piston is less than 1 bar, 1.0 – 0.1 = 0.9 bar. The valve is closed and the tank is heated back to room temperature. (Air can be considered an ideal gas with a T-independent CP = 29 J/mol-K.)
a. The useful work done by the process is the total work done by the piston in the expansion step less the amount of work done on the atmosphere. Calculate the useful work done per expansion stroke in kJ.
b. Calculate the amount of heat needed during the expansion in kJ. Neglect the heat capacity of the tank and cylinder.
c. Calculate the amount of cooling needed during the retraction of the cylinder in kJ.
3.11. A well-insulated tank contains 1 mole of air at 2 MPa and 673 K. It is connected via a closed valve to an insulated piston/cylinder device that is initially empty. The piston may be assumed to be frictionless. The volumes of the piping and valve are negligible. The weight of the piston and atmospheric pressure are such that the total downward force can be balanced with gas pressure in the cylinder of 0.7 MPa. The valve between the tank and piston/cylinder is cracked open until the pressure is uniform throughout. The temperature in the tank is found to be 499.6 K. Air can be assumed to be an ideal gas with a temperature-independent heat capacity CP = 29.3 J/mol-K.
a. What is the number of moles left in the tank at the end of the process?
b. Write and simplify the energy balance for the process. Determine the final temperature of the piston/cylinder gas.
3.12. A piston/cylinder has two chambers and includes a spring as illustrated below. The right-hand side contains air at 20°C and 0.2 MPa. The spring exerts a force to the right of F = 5500x N where x is the distance indicated in the diagram, and xi = 0.3 m. The piston has a cross-sectional area of 0.1 m2. Assume that the piston/cylinder materials do not conduct heat, and that the piston/cylinder and spring do not change temperature. After oscillations cease, what is the temperature of the air in the right chamber and the final position of the piston, xf, for the cases listed below? Use a temperature-independent heat capacity for air, CP = 7R/2.
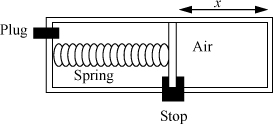
a. The left chamber is evacuated and the plug remains in place.
b. The plug is removed so that the left-side pressure stays at 0.1 MPa throughout the process.
3.13. We wish to determine the final state for the gas in an inflated balloon. Initially, the balloon has a volume of Vi at rest. The volume of the balloon is related to the internal pressure by V = a·P + b, where a and b are constants. The balloon is to be inflated by air from our lungs at Plung and Tlung which are known and assumed to remain constant during inflation. Heat transfer through the walls of the balloon can be ignored. The system is defined to be the gas inside the balloon at any time. Starting with the general energy balance, simplify to write the balance in terms of {CP, CV, Tlung, Plung, Ti, Tf, TR, PR} and either {Vi, Vf} or {Pi, Pf}. This will demonstrate that measurement of Vf or Pf is sufficient to determine Tf. Assume air is an ideal gas.CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply