In principle, most real systems are unsteady and open. A few systems couple the unsteady-state operation with flow across boundaries in a way that requires simultaneous analysis. We illustrate how to treat those systems with examples of leaking and filling tanks.
Example 2.15. Adiabatic expansion of an ideal gas from a leaky tank
An ideal gas is leaking from an insulated tank. Relate the change in temperature to the change in pressure for gas leaking from a tank. Derive an equation for ΔU for the tank.
Solution
Let us choose our system as the gas in the tank at any time. This will be an open, unsteady-state system. There is no inlet stream and one outlet stream. The mass balance gives dn = – dnout.
We can neglect kinetic and potential energy changes. Although the gas is expanding, the system size remains unchanged, and there is no expansion/contraction work. The energy balance becomes (on a molar basis):
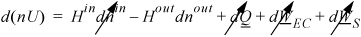
Since the enthalpy of the exit stream matches the enthalpy of the tank, Hout = H. d(nU) = –Houtdnout = Hdn. Now H depends on temperature, which is changing, so we are not able to apply hint 4(a) from the problem-solving strategy. It will be necessary to combine terms before integrating. By the product rule of differentiation, the left-hand side expands to d(nU) = ndU + Udn. Collecting terms in the energy balance,
ndU = (H – U)dn
Performing some substitutions, the energy balance can be written in terms of T and n,
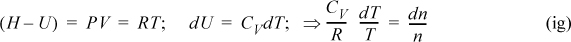

The volume of the tank is constant, (V = constant); therefore,
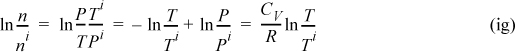
substituting,
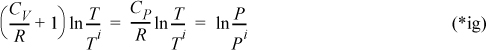
Recognizing the relation between CV and CP, defining γ≡ Cp/Cv (=1.4 for an ideal diatomic gas), note R/Cp = (Cp – CV)/CP = 1 – (1/γ) = (γ – 1)/γ:
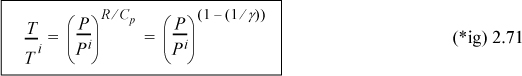
Through the ideal gas law (PV = RT), we can obtain other arrangements of the same formula.
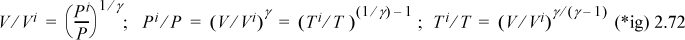
The numerical value for the change in internal energy of the system depends on the reference state because the reference state temperature will appear in the result:
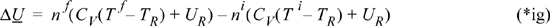
![]() For fluid exiting from an adiabatic tank, the results are the same as a closed system as in Example 2.11.
For fluid exiting from an adiabatic tank, the results are the same as a closed system as in Example 2.11.
At first glance, one might expect to use the same equation for a filling tank, but simply change the pressure ratio. Careful analysis shows that the energy balance is similar, but the final result is quite different.
Example 2.16. Adiabatically filling a tank with an ideal gas
Helium at 300 K and 3000 bar is fed into an evacuated cylinder until the pressure in the tank is equal to 3000 bar. Calculate the final temperature of the helium in the cylinder (CP/R = 5/2).
Solution
The system will be the gas inside the tank at any time. The system will be an open, unsteady-state system. The mass balance is dn = dnin. The energy balance becomes:
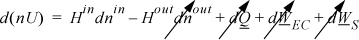
We recognize that Hin will be constant throughout the tank filling. Therefore, by hint 4a from the problem-solving strategy, we can integrate terms individually. We need to be careful to keep the superscript since the incoming enthalpy is at a different state than the system. The right-hand side of the energy balance can be integrated to give
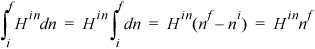
The left-hand side of the energy balance becomes
Δ(Un) = Ufnf – Uini = Ufnf
Combining the result with the definition of enthalpy,
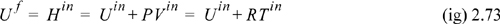
And with our definition of heat capacity, we can find temperatures:
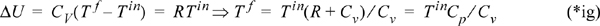
Note that the final temperature is independent of pressure for the case considered here.
You should not get the impression that unsteady, open systems are limited to ideal gases. Energy balances are independent of the type of operating fluid.
Example 2.17. Adiabatic expansion of steam from a leaky tank
An insulated tank contains 500 kg of steam and water at 215°C. Half of the tank volume is occupied by vapor and half by liquid; 25 kg of dry vapor is vented slowly enough that temperature remains uniform throughout the tank. What is the final temperature and pressure?
Solution
There are some similarities with the solution to Example 2.15 on page 81; however, we can no longer apply the ideal gas law. The energy balance reduces in a similar way, but we note that the exiting stream consists of only vapor; therefore, it is not the overall average enthalpy of the tank:
d(mU) = –Houtdmout = HV dm
The sides of the equation can be integrated independently if the vapor enthalpy is constant. Looking at the steam table, the enthalpy changes only about 10 kJ/kg out of 2800 kJ/kg (0.3%) along the saturation curve down to 195°C. Let us assume it is constant at 2795 kJ/kg making the integral of the right-hand side simply HVΔm. Note that this procedure is equivalent to a numerical integration by trapezoidal rule as given in Appendix B on page 822. Many students forget that analytical solutions are merely desirable, not absolutely necessary. The energy balance then can be integrated using hint 4a on page 74.
ΔU = mfUf – miUi = 2795(mf – mi) = 2795(–25) = –69,875 kJ
The quantity mf = 475, and miUi will be easy to find, which will permit calculation of Uf. For each m3 of the original saturated mixture at 215°C,

Therefore,
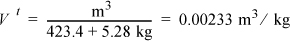
So the tank volume, quality, and internal energy are:

Then, from the energy balance and mass balance,
Uf = (–69,875 + 469,400) kJ / 475 kg = 841.0 kJ/kg
Vf = 1.166 m3 / 475 kg = 0.00245 m3/kg
We need to find Pf and Tf which correspond to these state variables. The answer will be along the saturation curve because the overall specific volume is intermediate between saturated vapor and liquid values at lower pressures. We will guess Pf (and the corresponding saturation Tf), find q from Vf, then calculate ![]() and compare to Uf = 841.0 kJ/kg. If
and compare to Uf = 841.0 kJ/kg. If ![]() is too high, the Pf (and Tf) guess will be lowered.
is too high, the Pf (and Tf) guess will be lowered.
Since V = VL + q(VV–VL),
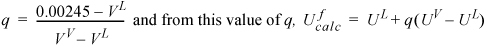
To guide our first guess, we need UL < Uf = 841.0 kJ/kg. Our first guess is Tf = 195°C. Values for the properties from the steam tables are shown in the table below. This initial guess gives Ufcalc = 845 kJ/kg; no further iteration is necessary. The HV at this state is 2789; therefore, our assumption of Hout ≈ constant is valid.

Leave a Reply