Several types of equipment are ubiquitous throughout industry, and facile abilities with the energy balance for these processes will permit more rapid analysis of composite systems where these units are combined. In this brief section we introduce valves and throttles used to regulate flow, nozzles, heat exchangers, adiabatic turbines and expanders, adiabatic compressors, and pumps.
Valves and Throttles
A throttling device is used to reduce the pressure of a flowing fluid without extracting any shaft work and with negligible fluid acceleration. Throttling is also known as Joule-Thomson expansion in honor of the scientists who originally studied the thermodynamics. An example of a throttle is the kitchen faucet. Industrial valves are modeled as throttles. Writing the balance for a boundary around the throttle valve, it is conventional to neglect any accumulation within the device since it is small relative to flow rates through the device, so the left-hand side is zero. At steady-state flow,
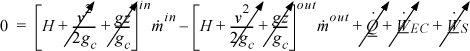
Changes in kinetic and potential energy are small relative to changes in enthalpy as we just discussed. When in doubt, the impact of changes in velocity can be evaluated as described in Example 2.9. The amount of heat transfer is negligible in a throttle. The boundaries are not expanding, and there is also no mechanical device for transfer of work, so the work terms vanish. Therefore, a throttle is isenthalpic:

Nozzles
Nozzles are specially designed devices utilized to convert pressure drop into kinetic energy. Common engineering applications involve gas flows. An example of a nozzle is a booster rocket. Nozzles are also used on the inlets of impulse turbines to convert the enthalpy of the incoming stream to a high velocity before it encounters the turbine blades.13 Δu is significant for nozzles. A nozzle is designed with a specially tapered neck on the inlet and sometimes the outlet as shown schematically in Fig. 2.7. Nozzles are optimally designed at particular velocities/pressures of operation to minimize viscous dissipation.
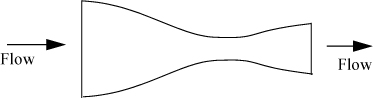
Figure 2.7. Illustration of a converging-diverging nozzle showing the manner in which inlets and outlets are tapered.
The energy balance is written for a boundary around the nozzle. Any accumulation of energy in the nozzle is neglected since it is small relative to flow through the device and zero at steady state. Velocity changes are significant by virtue of the design of the nozzle. However, potential energy changes are negligible. Heat transfer and work terms are dropped as justified in the discussion of throttles. Reducing the energy balance for a nozzle shows the following:
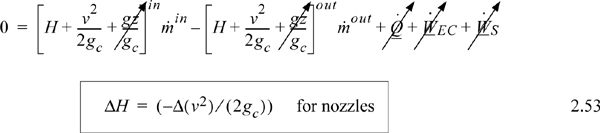
Properly designed nozzles cause an increase in the velocity of the vapor and a decrease in the enthalpy. A nozzle can be designed to operate nearly reversibly. Example 4.12 on page 162 describes a typical nozzle calculation.
Throttles are much more common in the problems we will address in this text. The meaning of “nozzle” in thermodynamics is much different from the common devices we term “nozzles” in everyday life. Most of the everyday devices we call nozzles are actually throttles.
Assessing when simplifications are justified requires testing the implications of eliminating assumptions. For example, to test whether a particular valve is acting more like a throttle or a nozzle, infer the velocities before and after the nozzle and compare to the enthalpy change. If the kinetic energy change is negligible relative to the enthalpy change then call it a throttle. Take note of the magnitude of the terms in the calculation so that you can understand how to anticipate a similar conclusion. For example, the volume change of a liquid due to a pressure drop is much smaller than that of a gas. With less expansion, the liquids accelerate less, making the throttle approximation more reasonable. This kind of systematic analysis and reasoning is more important than memorizing, say, that throttles are for liquids.
Heat Exchangers
Heat exchangers are available in a number of flow configurations. For example, in an industrial heat exchanger, a hot stream flows over pipes that carry a cold stream (or vice versa), and the objective of operation is to cool one of the streams and heat the other. A generic tube-in-shell heat exchanger can be illustrated by a line diagram as shown in Fig. 2.8. Tube-in-shell heat exchangers consist of a shell (or outer sleeve) through which several pipes pass. (The figure just has one pipe for simplicity.) One of the process streams passes through the shell, and the other passes through the tubes. Stream A in our example passes through the shell, and Stream B passes through the tubes. The streams are physically separated from one another by the tube walls and do not mix. Let’s suppose that Stream A is the hot stream and Stream B is the cold stream. In the figure, both streams flow from left to right. This type of flow pattern is called concurrent. The temperatures of the two streams will approach one another as they flow to the right. With this type of flow pattern, we must be careful that the hot stream temperature that we calculate is always higher than the cold stream temperature at every point in the heat exchanger.14 If we reverse the flow direction of Stream A, a countercurrent flow pattern results. With a countercurrent flow pattern, the outlet temperature of the cold stream can be higher than the outlet temperature of the hot stream (but still must be lower than the inlet temperature of the hot stream). The hot stream temperature must always be above the cold stream temperature at all points along the tubes in this flow pattern also.

Figure 2.8. Illustration of a generic heat exchanger with a concurrent flow pattern. The tube side usually consists of a set of parallel tubes which are illustrated as a single tube for convenience.
So far, our discussion has assumed that there are no phase transitions occurring in the heat exchanger. If Stream A is a hot stream, and Stream B is converted from liquid at the inlet to vapor at the outlet, we call the heat exchanger a boiler to bring attention to the phase transition occurring inside. The primary difference in the operation of a boiler to that of a generic heat exchanger is that the cold stream temperature change might be small or even zero. This is because the phase change will occur isothermally at the saturation temperature of the fluid corresponding to the boiler pressure, absorbing large amounts of heat. In a similar fashion, we could have Stream A be cooling water and Stream B be an incoming vapor which is condensed. We would call this heat exchanger a condenser, to clearly bring attention to the phase change occurring inside. In this case, the temperature change of the hot stream might be small. Another type of heat exchanger that we will use in Chapter 5 is the superheater. A superheater takes a vapor that is saturated and superheats it.
There are two more important points to keep in your mind as you perform thermodynamic calculations. For the purposes of this text we will neglect pressure drops in the heat exchangers; the outlet pressure will match the inlet pressure of Stream A, and a similar statement applies for Stream B. Note that this does not imply that streams A and B are at the same pressure. Also, we neglect heat transfer to or from the surroundings unless specified. Therefore, all heat transfer occurs inside the heat exchanger, not at the boundaries of the heat exchanger and the surroundings.
There are other configurations of heat exchangers such as kettle-type reboilers and plate-and-frame configurations; however, for thermodynamic purposes, only the flow pattern is important, not the details of material construction that lead to the flow pattern. Thus, the tube-in-shell concepts will be adequate for our needs.
The energy balance that we write depends on how we choose our system. Since the streams are physically separated from one another, we may write a balance for each of the streams independently, or we may place the system boundary around the entire heat exchanger and write a balance for both streams. Let us take the system to be Stream B and let us suppose that Stream B is boiled. In this case, there is just one inlet and outlet. There is no shaft work or expansion/contraction work. Even though the process fluid is expanding as it evaporates, the system boundaries are not expanding; expansion effects will be automatically included in the energy balance by the enthalpy terms which have the flow work embedded in them. If the system is operating at steady state, the left-hand side of the energy balance is zero,
![]() The energy balance for a heat exchanger may be written in several ways.
The energy balance for a heat exchanger may be written in several ways.
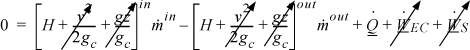
which simplifies to

where ![]() is the rate of heat transfer from the hot stream. On a molar (or mass) basis,
is the rate of heat transfer from the hot stream. On a molar (or mass) basis,
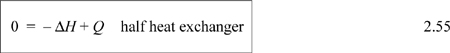
If we take the system boundaries to be around the entire heat exchanger, then there are multiple streams, and all heat transfer occurs inside, resulting in
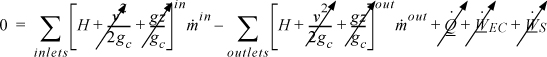
which simplifies to
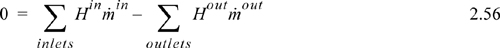

Since Eqns. 2.55 and 2.57 look quite different for the same process, it is important that you understand the placement of boundaries and their implications on the balance expression.
Adiabatic Turbines or Adiabatic Expanders
A turbine or expander is basically a sophisticated windmill as shown in Fig. 2.9. The term “turbine” implies operation by steam and the term “expander” implies operation by a different process fluid, perhaps a hydrocarbon, although the term “turbine” is used sometimes for both. The objective of operation is to convert the kinetic energy from a gas stream to rotary motion of a shaft to produce work (shaft work). The enthalpy of the high-pressure inlet gas is converted to kinetic energy by special stators (stationary blades) or nozzles inside the turbine shell. The high-velocity gas drives the rotor. Turbines are designed to be adiabatic, although heat losses can occur. When heat losses are present, they decrease the output that would have otherwise been possible for the turbine. Therefore, when calculations are performed, we assume that turbines or expanders operate adiabatically, unless otherwise noted.
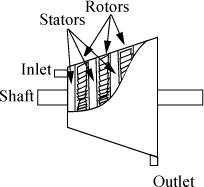
Figure 2.9. Illustration of a turbine. The rotor (shaft) turns due to the flow of gas. The blades connected to the shell are stationary (stators), and are sometimes curved shapes to perform as nozzles. The stator blades are not shown to make the rotors more clear.
The energy balance for the turbine only involves the kinetic energy change for the entering and exiting fluid, not for the changes occurring inside the turbine. Since the nozzles which cause large kinetic energy changes are inside the turbine unit, these changes are irrelevant to the balance around the unit. Recall from the development of our energy balance that we are only interested in the values of enthalpy, kinetic, and potential energy for streams as they cross the boundaries of our system. The energy balance for a steady-state turbine involving one inlet and one outlet is:
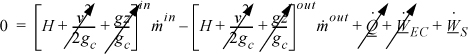
which becomes
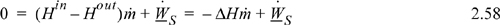
![]() Adiabatic turbine or expander.
Adiabatic turbine or expander.
and on a mass or molar basis becomes
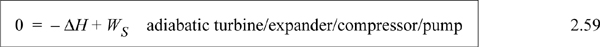
When we calculate values for the ΔH and work, they will be negative values.
Adiabatic Compressors
Adiabatic compressors can be constructed in a manner qualitatively similar to adiabatic turbines with stationary vanes (stators). This type of compressor is called an axial compressor. The main differences between turbines and axial compressors are: 1) the details of the construction of the vanes and rotors, which we won’t be concerned with; 2) the direction of flow of the fluid; and 3) the fact that we must put work into the compressor rather than obtaining work from it. Thus, the energy balance is the same as the turbine (Eqns. 2.58 and 2.59). When we calculate values for the ΔH and work, they will be positive values, where they were negative values for a turbine. Compressors may also be constructed as reciprocating (piston/cylinder) devices. This modification has no impact on our energy balance, so it remains the same. Analogous to turbines, it is conventional to assume that compressors are adiabatic unless otherwise noted.
Pumps
Pumps are used to move liquids by creating the pressure necessary to overcome the resistance to flow. They are in principle just like compressors, except the liquid will not change density the way a gas does when it is compressed. Again, the energy balance will be the same as a turbine or compressor (Eqns. 2.58 and 2.59). The primary difference we will find in application of the energy balance is that tabulated enthalpies are difficult to find for compressed liquids. Therefore, if we want to calculate the work needed for a pump, we can find it from the energy balance after we have calculated or determined the enthalpy change.
![]() Compressors and pumps usually have the same energy balance as turbines.
Compressors and pumps usually have the same energy balance as turbines.
Calculation of Shaft Work
Adiabatic steady-state turbines, compressors, and pumps all share a common energy balance, showing that the shaft work is related to the enthalpy change as shown on page 54. Often, it is helpful to calculate the shaft work directly and use the value of the shaft work to find the enthalpy change.
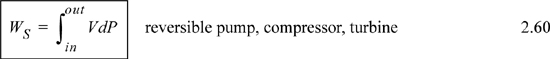
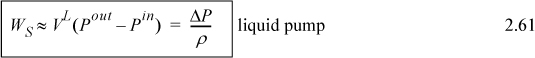
When the work is to calculated, the adiabatic shaft work may, in principle, be analyzed using ΔH or Eqn 2.60. For gases, it is usually easier to use other constraints to find the enthalpy change and then calculate the work by equality, though in principle the integral can be evaluated. For the special case of liquids, Eqn 2.60 can be replaced by Eqn. 2.61.
Leave a Reply