Reference States

Notice that our heat capacities do not permit us to calculate absolute values of internal energy or enthalpy; they simply permit us to calculate changes in these properties. Therefore, when is internal energy or enthalpy equal to zero—at a temperature of absolute zero? Is absolute zero a reasonable place to assign a reference state from which to calculate internal energies and enthalpies? Actually, we don’t usually solve this problem in engineering thermodynamics for the following two reasons:¹¹ 1) for a gas, there would almost always be at least two phase transitions between room temperature and absolute zero that would require knowledge of energy changes of phase transitions and heat capacities of each phase; and 2) even if phase transitions did not occur, the empirical fit of the heat capacity represented by the constants in the appendices are not valid down to absolute zero! Therefore, for engineering calculations, we arbitrarily set enthalpy or internal energy equal to zero at some convenient reference state where the heat capacity formula is valid. We calculate changes relative to this state. The actual enthalpy or internal energy is certainly not zero, it just makes our reference state location clear. If we choose to set the value of enthalpy to zero at the reference state, then H_R = 0, and U_R = H_R – (PV)_R where we use subscript R to denote the reference state. Note that U_R and H_R cannot be precisely zero simultaneously at the reference state. The reference state for water (in the steam tables) is chosen to set enthalpy of water equal to zero at the triple point. Note that PV is negligible at the reference state so that it appears that U_R is also zero to the precision of the tabulated values, which is not rigorously correct. (Can you verify this in the steam tables? Which property is set to zero, and for which state of aggregation?). To clearly specify a reference state we must specify:

1. The composition which may or may not be pure.

 Reference states permit the tabulation of values for U, H.

2. The state of aggregation (S, L, or V).

3. The pressure.

4. The temperature.

As you will notice in the following problems, reference states are not necessary when working with a pure fluid in a closed system or in a steady-state flow system with a single stream. The numerical values of the changes in internal energy or enthalpy will be independent of the reference state.

 Reference states are not required for steady-state flow systems with only a few streams, but are recommended when many streams are present.

When multiple components are involved, or many inlet/outlet streams are involved, definition of reference states is recommended since flow rates of the inlet and outlet streams will not necessarily match one-to-one. The reference state for each component may be different, so the reference temperature, pressure, and state of aggregation must be clearly designated.

For unsteady-state open systems that accumulate or lose mass, reference states are imperative when values of ΔU or ΔH changes of the system or surroundings are calculated as the numerical values depend on the reference state. It is only when the changes for the system and surroundings are summed together that the reference state drops out for unsteady-state open systems.

 Reference states are required for unsteady-state changes in U, H when mass accumulation is present.

Ideal Gas Properties

For an ideal gas, we must specify only the reference T and P.¹² An ideal gas cannot exist as a liquid or solid, and this fact completely specifies the state of our system. In addition, we need to set H_R or U_R (but not both!) equal to zero.

Also at all states, including the reference state, . The ideal gas approximation is reliable when contributions from intermolecular potential energy are relatively small. A convenient guideline is, in term of reduced temperature T_r = T/T_c, and reduced pressure P_r = P/P_c, where P_c is the critcal pressure.

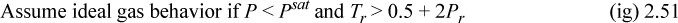
State Properties Including Phase Changes

Problems will often involve phase changes. Throughout a problem, since the thermodynamic properties must always refer to the same reference state, phase changes must be incorporated into state properties relative to the state of aggregation of the reference state. To calculate a property for a fluid at T and P relative to a reference state in another phase, a sketch of the pathway from the reference state is helpful to be sure all steps are included. Several pathways are shown in Fig. 2.6 for different reference states. Note that the ideal gas reference state with the generalized correlation for the heat of vaporization (option (c)) is convenient because it does not require liquid heat capacities. The accuracy of the method depends on the accuracy of the generalized correlation or the technique used to estimate the heat of vaporization. Option (c) is frequently used in process simulators. In some cases the user may have flexibility in specifying the correlation used to estimate the heat of vaporization.

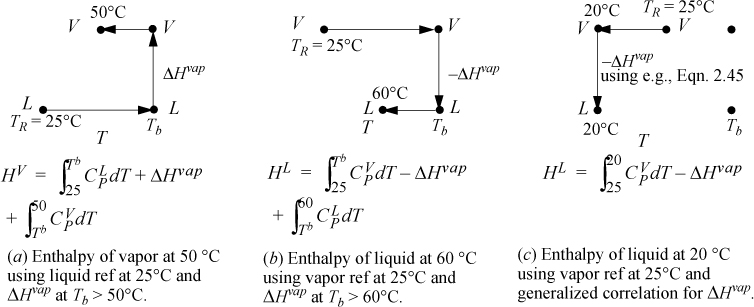
Figure 2.6. Illustrations of state pathways to calculate properties involving liquid/vapor phase changes. The examples are representative, and modified paths would apply for states above the normal boiling point, T_b. Similar pathways apply for solid/liquid or solid/vapor transformations. Note that a generalized correlation is used for ΔH^vap which differs from the normal boiling point value. The method is intended to be used at subcritical conditions. Pressure corrections are not illustrated for any paths here.

---

Example 2.8. Acetone enthalpy using various reference states

Calculate the enthalpy values for acetone as liquid at 20°C and vapor at 90°C and the difference in enthalpy using the following reference states: (a) liquid at 20°C; (b) ideal gas at 25°C and ΔH^vap at the normal boiling point; (c) ideal gas at 25°C and the generalized correlation for ΔH^vap at 20°C. Ignore pressure corrections and treat vapors as ideal gases.

Solution

Heat capacity constants are available in Appendix E. For all cases, 20°C is 293.15K, 90°C is 363.15K, and the normal boiling point is T_b = 329.15K.

a. H^L = 0 because the liquid is at the reference state. The vapor enthalpy is calculated analogous to Fig. 2.6, pathway (a). The three terms of pathway (a) are H^V = 4639 + 30200 + 2799 = 37,638 J/mol. The difference in enthalpy is ΔH = 37,638 J/mol.

b. H^L will use a path analogous to Fig. 2.6, pathway (b). The three terms of pathway (b) are H^L = 2366 – 30200 – 4638 = –32472 J/mol. H^V is calculated using Eqn. 2.50, H^V = 5166 J/mol. The difference is ΔH = 5166 + 32472 = 37,638 J/mol, same as part (a).

c. H^L will use a path analogous to Fig. 2.6, pathway (c). The generalized correlation of Eqn. 2.45 predicts a heat of vaporization at T_b of 29,280 J/mol, about 3% low. At 20°C, the heat of vaporization is predicted to be 31,420 J/mol. The two steps in Fig. 2.6 (c) are H^L = –365 – 31420 = –31785 J/mol. The enthalpy of vapor is the same calculated in part (b), H^V = 5166 J/mol. The enthalpy difference is ΔH = 5166 + 31785 = 36,950 J/mol, about 2% low relative to part (b).