A closed system is one in which no mass flows in or out of the system, as shown in Fig. 2.3. The introductory sections have discussed heat and work interactions, but we have not yet coupled these to the energy of the system. In the transformations we have discussed, energy can cross a boundary in the form of expansion/contraction work (–∫ PdV), shaft work (WS), and heat (Q)4. There are only two ways a closed system can interact with the surroundings, via heat and work interactions. If we put both of these possibilities into one balance equation, then developing the balance for a given application is simply a matter of analyzing a given situation and deleting the balance terms that do not apply. The equation terms can be thought of as a check list.
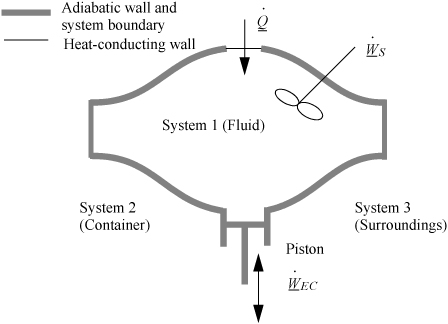
Figure 2.3. Schematic of a closed system.
A closed system interacts with the surroundings only through heat and work.
Experimentally, scientists discovered that if heat and work are measured for a cyclical process which returns to the initial state, the heat and work interactions together always sum to zero. This is an important result! This means that, in non-cyclical processes where the sum of heat and work is non-zero, the system has stored or released energy, depending on whether the sum is positive or negative. In fact, by performing enough experiments, scientists decided that the sum of heat and work interactions in a closed system is the change in energy of the system! To develop the closed-system energy balance, let us first express the balance in terms of words.
Energy within the system is composed of the internal energy (e.g., U), and the kinetic (mu2/2gc) and potential energy (mgz/gc) of the center of mass. For closed systems, the “check list” equation is:
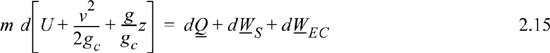
The left-hand side summarizes changes occurring within the system boundaries and the right-hand side summarizes changes due to interactions at the boundaries. It is a recommended practice to always write the balance in this convention when starting a problem. We will follow this convention throughout example problems in Chapters 2–4 and relax the practice subsequently. The kinetic and potential energy of interest in Eqn. 2.15 is for the center of mass, not the random kinetic and potential energy of molecules about the center of mass. The balance could also be expressed in terms of molar quantities, but if we do so, we need to introduce molecular weight in the potential and kinetic energy terms. Since the mass is constant in a closed system, we may divide the above equation by m,
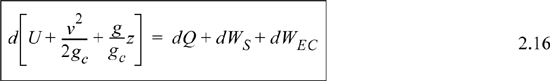
Closed-system balance. The left-hand side summarizes changes inside the boundaries, and the right-hand side summarizes interactions at the boundaries.
where heat and work interactions are summed for multiple interactions at the boundaries. We can integrate Eqn. 2.16 to obtain
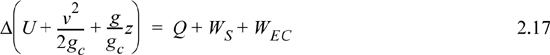
We may also express the energy balance in terms of rates of change,
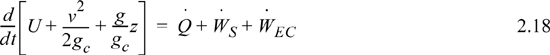
where , 
and Frequently, the kinetic and potential energy changes are small (as we will show in Example 2.9), in a closed system shaft work is not common, and the balance simplifies to
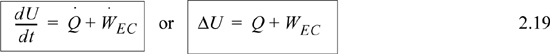
Example 2.3. Internal energy and heat
In Section 2.5 on page 46 we discussed that heat flow is related to the energy of system, and now we have a relation to quantify changes in energy. If 2000 J of heat are passed from the hot block to the cold block, how much has the internal energy of each block changed?
Solution
First choose a system boundary. Let us initially place system boundaries around each of the blocks. Let the warm block be block1 and the cold block be block2. Next, eliminate terms which are zero or are not important. The problem statement says nothing about changes in position or velocity of the blocks, so these terms can be eliminated from the balance. There is no shaft involved, so shaft work can be eliminated. The problem statement doesn’t specify the pressure, so it is common to assume that the process is at a constant atmospheric pressure of 0.101 MPa. The cold block does expand slightly when it is warmed, and the warm block will contract; however, since we are dealing with solids, the work interaction is so small that it can be neglected. For example, the blocks together would have to change 10 cm3 at 0.101 MPa to equal 1 J out of the 2000 J that are transferred.
Therefore, the energy balance for each block becomes:
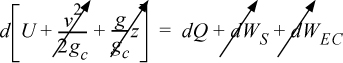
We can integrate the energy balance for each block:
The magnitude of the heat transfer between the blocks is the same since no heat is transferred to the surroundings, but how about the signs? Let’s explore that further. Now, placing the system boundary around both blocks, the energy balance becomes:
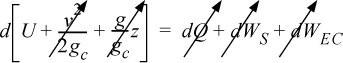
Note that the composite system is an isolated system since all heat and work interactions across the boundary are negligible. Therefore, ΔU = 0 or by dividing in subsystems, ΔUblock1 + ΔUblock2 = 0 which becomes ΔUblock1 = –ΔUblock2. Notice that the signs are important in keeping track of which system is giving up heat and which system is gaining heat. In this example, it would be easy to keep track, but other problems will be more complicated, and it is best to develop a good bookkeeping practice of watching the signs. In this example the heat transfer for the initially hot system will be negative, and the heat transfer for the other system will be positive. Therefore, the internal energy changes are ΔUblock1 = –2000 J and ΔUblock2 = 2000 J.
Although very simple, this example has illustrated several important points.
1. Before simplifying the energy balance, the boundary should be clearly described by a statement and/or a sketch.
2. A system can be subdivided into subsystems. The composite system above is isolated, but the subsystems are not. Many times, problems are more easily solved, or insight is gained by looking at the overall system. If the subsystem balances look difficult to solve, try an overall balance.
3. Positive and negative energy signs are important to use carefully.
4. Simplifications can be made when some terms are small relative to other terms. Calculation of the expansion contraction work for the solids is certainly possible above, but it has a negligible contribution. However, if the two subsystems had included gases, then this simplification would have not been reasonable.
Leave a Reply