In engineering applications, most problems involve flowing systems. This means that materials typically flow into a piece of equipment and then flow out of it, crossing well-defined system boundaries in the process. Thus, we need to introduce an additional characterization of work: the work interaction of the system and surroundings when mass crosses a boundary. For example, when a gas is released out of a tank through a valve, the exiting gas pushes the surrounding fluid, doing work on the surroundings. Likewise, when a tank valve is opened to allow gas from a higher pressure source to flow inward, the surroundings do work on the gas already in the system. We calculate the work in these situations most easily by first calculating the rate at which work is done.
Let us first consider a fluid entering a system as shown in Fig. 2.1. We have dW = Fdx, and the work interaction of the system is positive since we are pushing fluid into the system. The rate of work is 
, but 
is velocity, and F = P·A. Further rearranging, recognizing 
, and that the volumetric flow rate may be related to the mass specific volume and the mass flow rate, 
,
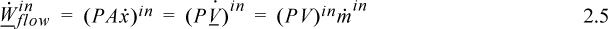
Work associated with fluid flowing in/out of boundaries is called flow work.
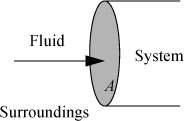
Figure 2.1. Schematic illustration of flow work.
where PV are the properties of the fluid at the point where it crosses the boundary, and 
is the absolute value of the mass flow rate across the boundary. When fluid flows out of the system, work is done on the surroundings and the work interaction of the system is
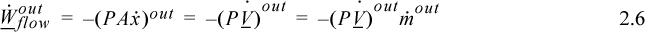
where 
is the absolute value of the mass flow across the boundary, and since work is being done on the surroundings, the work interaction of the system is negative. When flow occurs both in and out, the net flow work is the difference:
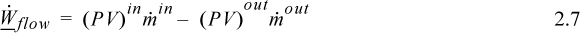
where and are absolute values of the mass flow rates. For more streams, we simply follow the conventions established, and add inlet streams and subtract outlet streams.
Leave a Reply