As interconversion between heat and work is the central concern of thermodynamics, it is useful to define thermodynamic properties that are related to the heat content of a system and energy available for conversion to work. This consideration leads to three thermodynamic functions or properties that are mathematically defined as follows:
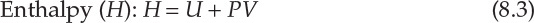
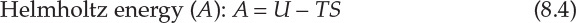
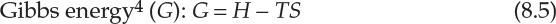
4. The terms Helmholtz function (or Helmholtz energy) and Gibbs function (or Gibbs energy) are preferred over classical usage of terms Helmholtz free energy and Gibbs free energy. Helmholtz function is named after Herrmann Helmholtz, another central founder of the discipline of thermodynamics.
In these equations, P, V, and T are the pressure, volume, and temperature of the system.
Enthalpy of a system is a measure of its heat content, which was discussed in Chapter 7, “Energy Balance Computations.” The significances of the two thermodynamic properties are best understood in terms of changes in the values of A and G. Simply stated, the change in Helmholtz energy represents the maximum amount of work that can be obtained from the system, whereas the change in Gibbs energy represents the maximum amount of work that can be extracted from the system excluding any work of expansion. Mathematically [6], this is as follows:


Here, Wmax represents the maximum work that can be extracted from the system. Equations 8.6 and 8.7 indicate that any work extracted from the system (done by the system) is at the expense of the Helmholtz energy and Gibbs energy, respectively. Gibbs energy is also the key thermodynamic property in determination of system equilibrium, as will be discussed later.
Leave a Reply