A chemical engineer has to perform a wide variety of energy balance computations for a large number of transformations and processes. These computations require application of the principles discussed in section 7.1. The myriad energy balance computations performed by chemical engineers can very broadly be classified into two types: those involving determination of heat effects in particular transformations of interest and those involving determinations of system temperatures as a result of the particular transformation undergone by the system. The following examples provide a brief glimpse into the nature of energy balance computations for different chemical processes.
EXAMPLE 7.2.1 ADIABATIC FLAME TEMPERATURE OF EXHAUST GASES
Consider again the material balance discussed in example 6.3.1, the combustion of natural gas. Burning the natural gas releases heat—a manifestation of the principle of the conservation of energy, where the chemical energy stored in methane is converted into chemical energy of products and thermal energy. If this heat is not removed from the system, then it would cause the temperature of the product stream to rise. Adiabatic flame temperature in a combustion process is simply the theoretical temperature reached by the product gases in a combustion process, when the process is conducted adiabatically—without any energy exchange with the surroundings. Calculate the adiabatic flame temperature for complete combustion of natural gas when stoichiometric quantity of air is fed to the burner. All the inlet streams are at 25°C.
Solution
The first step in performing energy balance computations is obtaining the material balance for the process. These material balance calculations were conducted in Chapter 6 and are reproduced in Figure 7.4.
Figure 7.4 Material balance on a natural gas burner.
Note that Figure 7.4 shows the material balance for a continuous process where 1 mol/s of the natural gas is fed to the burner continuously. Since the process is adiabatic, at steady state the enthalpy flowing into the burner must equal the enthalpy leaving the burner:
The enthalpy flowing in is equal to the sum of enthalpies carried into the burner by the three components:
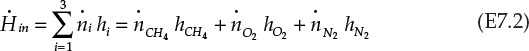
Here, 
represents the molar flow rate of component i, and hi its specific enthalpy (enthalpy per mole).
Similarly, the enthalpy flowing out of the burner is the sum of enthalpies of the components exiting the burner:
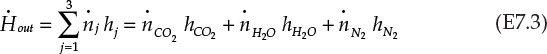
Enthalpies in equations E7.2 and E7.3 are evaluated at the corresponding stream temperatures; that is, at 25°C (298.15 K) for the inlet streams and an unknown temperature T (K) for the product stream. As mentioned earlier, enthalpies at 298.15 K are the enthalpies of formation at the standard state and are available from various sources. The enthalpies hj can be expressed in terms of this temperature T, making use of equation E7.4:
Table E7.1 shows the standard enthalpies of formation (
), and Table E7.2 shows the functional dependence of the heat capacity for each component [3, 7].
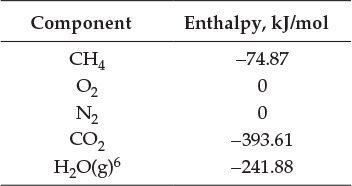
Table E7.1 Standard Enthalpies of Formation
Table E7.2 Functional Dependence of Heat Capacity
Using this data, the rate of enthalpy fed to the system (
) is found to be equal to -74.87 kJ/s. The rate at which enthalpy is leaving the system is calculated as follows:6
6. Gas phase.
First, the specific enthalpy of each species at temperature T is calculated from the CP data:
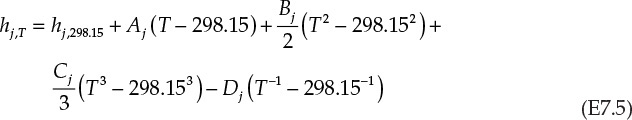
Substituting equation E7.5 in equation E7.3 and rearranging terms gives us the following:
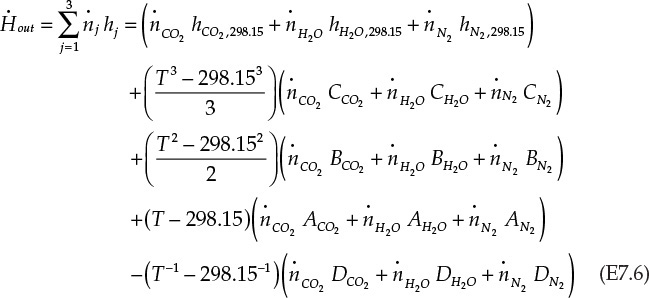
Equation E7.6 appears complicated, but that is primarily because all the individual terms are written in expanded form rather than because of any intrinsic complexity.
The molar flow rates of components in the outlet stream are as shown in Figure 7.4. Equating 
to -74.87 kJ/s, and substituting the values of various parameters yields the following equation in unknown outlet temperature T:
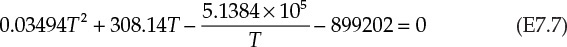
Equation E7.7 is a polynomial equation that can be solved using a number of different techniques. The solution using the Goal Seek tool in Microsoft Excel (described in Chapter 5, “Computations in Fluid Flow”) is shown in Figure 7.5.
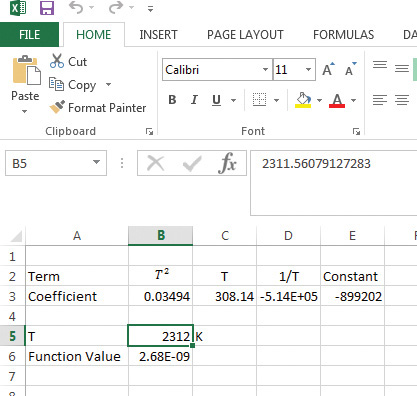
Figure 7.5 Excel Goal Seek solution for adiabatic flame temperature problem.
As seen from the figure, the coefficients of the terms T2, T, and 1/T are entered in cells B3, C3, and D3, with the constant value in the cell E3. A temperature guess is provided in cell B5, and the function described by equation E7.7 is evaluated in cell B6. The Goal Seek function manipulates the value in B5 until the function value in B6 is approximately zero. The adiabatic flame temperature is 2312 K (~2039°C).
The graphical solution for the problem using Mathcad is shown in Figure 7.6.
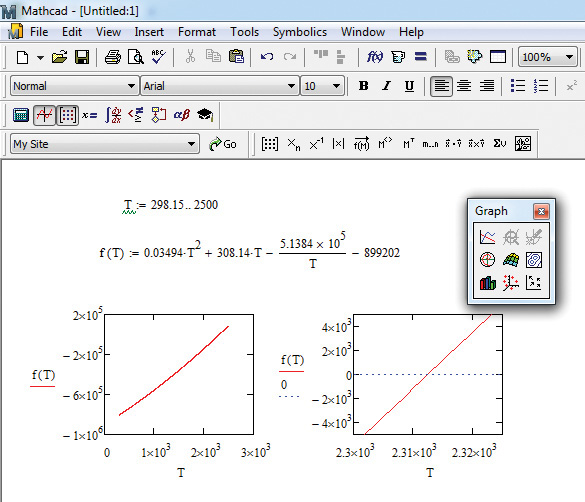
Figure 7.6 Mathcad graphical solution of the adiabatic flame temperature problem.
The steps for obtaining the solution are as follows:
1. First, define a range for variable T by typing T:298.15;2500.
2. Define the function f(T) by typing
f(T):0.03494*T^2 +308.14*T-5.1384*10^5/T-899202
3. Create the graph of f(T) as a function of T by choosing Insert from the command menu, and then Graph and X-Y Plot from the dropdown menus. (Alternatively, a graph can also be created by clicking on the appropriate buttons.) This creates a blank graph with empty placeholders for the x and y variables. Enter T and f(T) by clicking on these placeholders, generating the graph shown at the bottom on the left. As can be seen from the graph, the function value goes from ~-8 × 105 to ~1.6 × 105, indicating that function value is zero in the vicinity of T = 2000. To get an accurate estimate, replot the function, as shown on the right, with the x-axis values between 2300 and 2325. In addition, add a straight horizontal line at y = 0 by clicking at the end of y-axis label f(T) and typing a space followed by 0.
4. The graph on the right clearly shows that the function is zero (from the intersection of the function curve with the horizontal dashed line) at a T value between by 2310 and 2315, enabling a guess for the solution at 2312. Improve the accuracy of the solution by progressively rescaling the x-axis to narrow the limits. However, it should be noted that a solution guess of 2310 is already within 0.1% of the exact solution and is adequate for most practical purposes.
EXAMPLE 7.2.2 HEAT RECOVERY FROM COMBUSTION GASES
The combustion gases from the burner in the previous example are cooled to 25°C, in the process heating up water to 150°F (as would happen in a water heater). What is the flow rate of hot water if the cold water entering the heater is at 68°F?
Solution
The schematic of the process is shown in Figure 7.7.
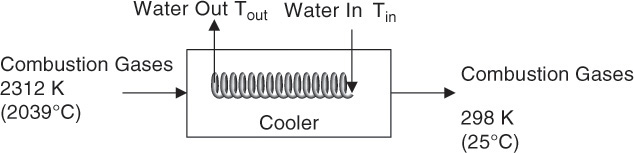
Figure 7.7 Energy balance on a water heater.
As seen from the figure, the water is passed through the inside of the pipe, which is shaped into a coil to provide the necessary area for heat exchange. The energy balance on the process yields the following equation:
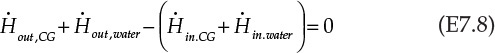
CG stands for combustion gases. Rearranging the terms in Equation E7.8 gives us the following:
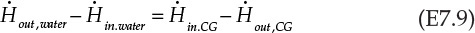
Equation E7.9 is the mathematical expression stating that the rate of enthalpy change for combustion gases is exactly equal to the rate of enthalpy change for water; that is, all the energy lost by the combustion gases is transferred to water. An assumption implicit in this statement is that the heater is perfectly insulated and there is no heat loss to the surroundings. The rate of enthalpy flowing in with the combustion gases, 
, is -74.87 kJ/s, using the information from Example 7.2.1. The other terms in the equation E7.9 are calculated as follows:
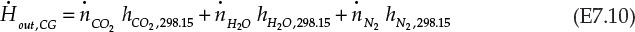
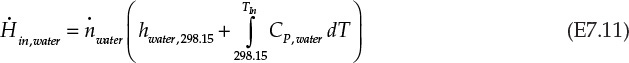
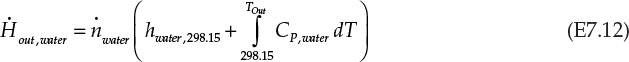
From equation E7.11 and E7.12, the right side of equation E7.9 is simplified:
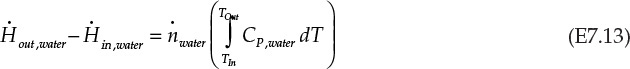
Using the enthalpies of formation data from Example 7.2.1, the left side of equation E7.9 is found to be 802.5 kJ/s. Assuming a constant specific heat capacity of 4.185 J/g K for water, the energy balance simplifies to the following:
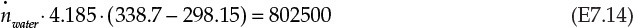
The inlet and outlet temperatures are expressed in the units of K rather than °F. The mass flow rate of water, 
, is readily calculated from equation E7.14 to be 4210 g/s. The volumetric flow rate of water is 4.21 L/s at a density of 1 g/cm3 (1 kg/L).
Note that the calculations in this example are based on the assumption that all the components in outlet combustion gases remain in the gaseous state at 25°C. While this assumption is valid for nitrogen and carbon dioxide, it does not hold true of water, which will condense into liquid when cooled below 100°C at atmospheric pressure. If it is assumed that all of the water vapor present in the combustion gases condenses at 25°C,7 then the standard enthalpy of formation of liquid water, -285.8 kJ/mol, should be used in the calculations instead of -241.88 kJ/mol for water vapor. This yields a water flow rate of 4671 g/s, or 4.67 L/s, as the answer. The reader is left to work out the computations to confirm the result.
7. In reality, not all of the water vapor will condense. This situation is dealt with in Chapter 8, “Computations in Chemical Engineering Thermodynamics.”
EXAMPLE 7.2.3 CALCULATION OF HEAT TRANSFER AREA8
8. Calculations related to heat transfer are covered in the engineering thermodynamics and transport phenomena courses and typically are not covered in the sophomore-level material and energy balance course.
How much heat transfer area needs to be provided in order to achieve the desired outlet temperatures in the above problem?
Theoretical background
Heat exchange equipment is an integral and ubiquitous component in chemical process industries. Many process streams need to be heated to desired temperatures for conducting reactions and effecting separations. Several other process streams need to be cooled from high temperatures for proper handling of product streams and emissions to the environment. Most of this heat exchange requirement is met through recuperators—heat exchangers in which a flowing hot stream transfers heat to a cold stream across a barrier that keeps the two streams physically separated [8]. The driving force for this heat transfer is the temperature difference between the two streams. The thermal duty of the heat exchanger, 
, is related to the driving force:
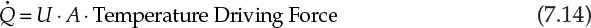
Here, A is the heat transfer area, and U is the overall heat transfer coefficient.
The overall heat transfer coefficient U is a measure of rate at which heat is transferred across a surface. A higher value of U implies faster heat transfer, and consequently the area needed is lower. U depends on the properties of the fluid and the operating conditions—mainly the fluid velocity. The temperature driving force depends on the difference in the temperatures of the two fluids between which heat is transferred. This driving force varies with the location within the heat exchanger as the temperatures of both fluids are changing. The overall driving force is then obtained by taking a logarithmic mean of the temperature differences at the inlet and the outlet of the heat exchanger.9 For the situation shown in Figure 7.7, the log-mean temperature difference (LMTD or ΔTLM) is given by equation 7.15:
9. The development of the concept of the log-mean temperature difference is discussed in engineering thermodynamics and transport phenomena courses.
Solution
Rearranging equation 7.14 gives us the following equation:
The thermal duty of the heat exchanger, , was found earlier in Example 7.2.2 to be 802500 W (J/s). The temperature driving force, ΔTLM, follows:
The overall heat transfer coefficient, as previously mentioned, depends on the properties of the fluids and the operating conditions. Various empirical and semi-empirical correlations are available in various literature for the estimation of the heat transfer coefficients under different combinations of cold and hot fluids, types of operation, and so on. Approximate values of typical heat transfer coefficients when the detailed information about the fluids and operating conditions is not available are also available in literature. Using a representative value of 300 W/m2 K for U, the area needed is found to be 8.13 m2. If the water is flowing through a 1 in. diameter pipe, then the length of the pipe needed to obtain this area is 8.13/(p · 0.0254),10 almost 101 m.
10. Heat transfer takes place across the surface area of the pipe, which is equal to pdL for a pipe having a diameter d and length L.
EXAMPLE 7.2.4 HEAT EFFECTS IN A CHEMICAL REACTION
Calcium oxide is mixed with water in a process called slaking to obtain calcium hydroxide. In a batch tank at 25°C, 3000 kg CaO are mixed with 3000 kg water. What is the heat evolved in the reaction? The standard enthalpies of formation are CaO(s): -635.1 kJ/mol; water: -285.8 kJ/mol; and Ca(OH)2 (aq): -1002.8 kJ/mol. The molar masses (g/mol) of the three substances are 56.1, 18.0, and 74.1, respectively.
Solution
The process is represented by the following equation:
CaO(s)+ H2O → Ca(OH)2 (aq)
The enthalpy change in the reaction per mole of CaO follows:
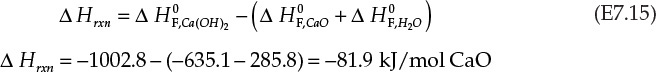
The negative sign associated with the enthalpy (heat) of the reaction indicates that the product has lower energy compared to the reactants. The difference between the two enthalpies appears as heat that is rejected to the surroundings, making this an exothermic process. For every mole of CaO converted to Ca(OH)2, 81.9 kJ heat is evolved. The total heat evolved is obtained by multiplying it by the total number of moles of CaO fed to the process:
Heat evolved = 81.9 kJ/mol · 3000 kg · 1000 g/kg /56.1 g/mol = 4380 MJ
This is a substantially large quantity of heat, which, if not removed from the system, will result in an increase in the temperature of the solution.
Assuming the specific heat capacity of the solution to be 4.185 MJ/ton K (4.185 J/g K),11 the temperature rise would be 4380/(4.185 × 6) = 174 K (°C), causing the solution temperature to rise to ~200°C. This is physically impossible, as water will start boiling off from the solution at 100°C at atmospheric pressure. So, in reality, the solution temperature will increase until it reaches 100°C (more accurately, the boiling point of the solution, which would be somewhat higher due to the colligative properties),12 when boil-off of water will commence. The amount of water boiling off can be calculated as follows:
11. A gross simplification, as this value is the specific heat capacity of water, and the system consists of a highly concentrated solution.
12. Colligative properties are solution properties that depend on the amount of solute present in the solution.
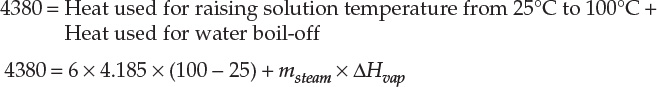
Here, msteam is the mass of the steam generated, and ΔHvap is the latent heat of vaporization (2260 J/g or MJ/ton). Therefore, the amount of steam generated, or water boil-off, is 1.105 ton or 1105 kg. The complete material and energy balances for the system are shown in Figure 7.8.
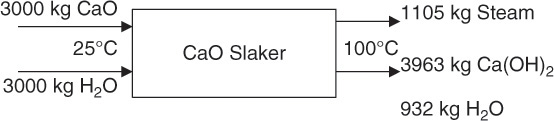
Figure 7.8 Material and energy balance on a CaO slaking operation.
As can be seen from the figure, slaking the lime yields two products: 1105 kg steam and Ca(OH)2 containing ~19% moisture.
Leave a Reply