Reacting systems are characterized by the disappearance of reactants and appearance of the products. Clearly, molecular species are not conserved in the reaction, and at steady state, the rate of input of a compound participating in the reaction is not equal to the rate of its output. However, as long as no nuclear reactions are occurring in the system, atomic species are conserved. Therefore, the approach to obtaining the material balance in a reacting system involves formulating independent conservation equations for the atoms of elemental species involved in the reactions [4]. It should also be noted that several inert species that do not participate in the reaction are often present in a reacting system, and the material balance for such species can be expressed in terms of molecular quantities. For example, if a combustion reaction is conducted using air as the oxidant, then the nitrogen (N2) present in air does not participate in the reaction and is treated as an inert. Similarly, solvents employed for liquid-phase reactions—water for aqueous phase reactions, for example—do not participate in the reaction, and the material balance for these inert solvents may be written in terms of molecular species.
Conducting a material balance on a reacting system requires a knowledge of the balanced chemical equation(s) for the reaction(s). The chemical equation provides the information about the proportions of the different species involved in the reaction—the stoichiometry of the reaction. Let us consider a general reaction involving species A, B, C, and D according to the equation:

where a, b, c and d are the stoichiometric coefficients of the species A, B, C, and D, respectively. According to this equation, the ratio of the amount of C formed (molecules or moles) to the amount of A reacting will be equal to c/a. Similarly, proportional quantities of D are formed and B are reacted, depending on the stoichiometric coefficients d and b, respectively. Example 6.3.1 illustrates the application of these principles to a simple reacting system involving a single reaction.
EXAMPLE 6.3.1 COMBUSTION OF NATURAL GAS
Natural gas is burned in a reactor (such as in a typical gas water heater in a home) using air as the oxidant. Calculate the quantities of air needed and the products formed per mole of the natural gas burned in the system.
Solution
Obtaining the material balance for this system requires knowledge of the chemicals present in the natural gas. Natural gas is, in reality, a mixture of gases dominated by methane (CH4). However, in these calculations, it is assumed that the natural gas is composed entirely of CH4. This assumption allows us to simplify the system and write a single chemical reaction to represent the combustion. Complete combustion of CH4 results in the formation of carbon dioxide (CO2) and H2O according to the following equation:
CH4 + 2O2 → CO2 + 2H2O
From the equation, the stoichiometric proportions between various species are obtained as follows:
O2/CH4 = 2, CO2/CH4 = 1, and H2O/CH4 = 2
Therefore, two moles of oxygen (O2) are needed per mole of natural gas, and the 3 moles of product are formed that include 1 mole of CO2 and 2 moles of H2O. Since the O2 supplied is obtained from air, the system also contains N2.3 The amount of N2 associated with O2 is equal to 2 (mol O2) ∙ 79/21 (mole ratio of N2 to O2 in air), that is, 7.52 moles per mole of natural gas. All of this N2 passes unreacted through the system and exits with the product gas. The complete material balance for the system is shown in Figure 6.4.
3. This is a simplifying assumption regarding the composition of air. Obviously, air has many more constituents in addition to O2 and N2. However, unless required by rigorous specifications, the trace constituents are neglected and air is considered as a mixture of N2 and O2 with the molar ratio of N2 to O2 being 79/21 (= 3.76).

Figure 6.4 Material balance on a natural gas burner.
It can be seen that all the CH4 and O2 fed to the burner react completely and are not present in the outlet product stream. This is an idealized representation, because an actual operating burner may have some inefficiencies that result in incomplete combustion of CH4—which will result in some unreacted CH4 being present in the product stream, or more likely, some fraction of the CH4 fed is converted to carbon monoxide (CO) rather than CO2. In any case, there will be unreacted O2 present in the product stream. Further, excess O2 is typically provided in combustion reactions to accomplish a complete conversion of the fuel. These situations will result in a material balance modified as follows:
Modification 1 Excess Air Supplied
Rework the material balance when the air supplied is 15% in excess of the stoichiometric requirements.
Solution
The stoichiometric O2 requirement is as given by the previous equation:
Stoichiometric O2 requirement: 2 moles/mole of CH4
Total O2 supplied: 2.30 (= 2 × 1.15) moles/mole of CH4
Total N2 fed with O2: 8.65 (= 2.30 × 79/21) moles/mole CH4
This N2 will pass unreacted through the system, ending up in the product stream along with 1 mole of CO2 and 2 moles of H2O formed from CH4. In addition, the product stream will contain unreacted O2, the quantity of which is 0.30 moles (2.30 moles fed—2 moles reacted according to the equation). The resulting material balance is shown in Figure 6.5.

Figure 6.5 Material balance on a natural gas burner—excess air.
Modification 2 Excess Air Supplied and Incomplete Combustion of Methane
Rework the material balance when 1% of the CH4 fed does not react in the burner. Further, of the CH4 burned, only 90% undergoes complete combustion. Fifteen percent excess air is supplied.
Solution
The product gas mixture will now contain a total of six components: unreacted CH4, CO2, CO, H2O, N2, and O2. The quantity of air fed is that calculated earlier for modification 1. To calculate the quantities of various species formed and O2 reacted and remaining, a balanced chemical equation for incomplete combustion of CH4 (formation of CO, rather than CO2) is needed:
CH4 + 1.5O2 → CO + 2H2O
From the given information, 1% of CH4 does not burn, so CH4 in the product stream is equal to 0.01 moles; 0.99 moles of CH4 react, 90% according to the equation corresponding to complete combustion and 10% according to that corresponding to incomplete combustion to CO. Therefore,
CO2 formed: 0.99 × 0.90 = 0.891 moles
CO formed: 0.99 × 0.10 = 0.099 moles
H2O formed: 0.99 × 0.90 × 2 + 0.99 × 0.10 × 2 = 1.98 moles
O2 reacted: 0.99 × 0.90 × 2 + 0.99 × 0.10 × 3/2 = 1.9305 moles
Hence, unreacted O2 = 2.30 – 1.9305 = 0.3695 moles. Figure 6.6 shows the resulting material balance.
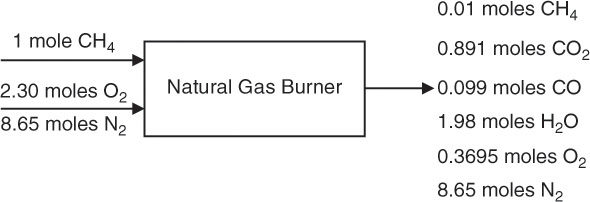
Figure 6.6 Material balance on a natural gas burner—excess air and incomplete combustion.
This solution was obtained through stoichiometric proportions given by the two equations. Atomic species balances are implicit in these proportions. The same solution can be obtained through explicit atomic species balances. For example, the amounts of O2 and N2 in the feed are calculated as before. The amounts of various species in the outlet stream are unknown at this point and are denoted by unknown variables: n1 (moles of CH4), n2 (moles of CO2), n3 (moles of CO), n4 (moles of H2O), n5 (moles of O2), and n6 (moles of N2). Balance on each of the atomic species (C, H, O, and N) yield the following four equations:


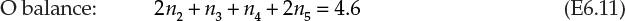

Equation E6.12 yields the moles of N2 in the outlet, n6, directly as 8.65, leaving three equations (E6.9, E6.10, and E6.11) in five unknowns. This system of equations cannot be solved unless more information provided in the problem statement is used to formulate two additional equations.4 The first equation is obtained from the information that only 99% of the CH4 is reacted. Since 1% of CH4 has not reacted, the following applies:
4. The degrees of freedom analysis, typically covered in the material and energy balances course, discusses in detail the relationship between unknown variables, mass balance equations, and other equations and specifications needed for complete material and energy balance solution for the system. Here, we simply try to formulate as many equations as there are unknown variables.(Continues)

The second equation is obtained from the information that 90% of the CH4 reacted undergoes complete combustion (it is converted to CO2), and the remaining 10% undergoes incomplete combustion (it is converted to CO). Therefore, the molar ratio between CO2 to CO must be 9:

Equations E6.9, E6.10, E6.11, E6.13, and E6.14 form a system of five equations in five unknowns that are rewritten in matrix form as follows (equation E6.14 is reformatted as n2 – 9n3 = 0 before entering it into the matrix form):

Equation E6.15 conforms to the matrix form [A][X] = [B] for simultaneous linear equations, where [A] is the matrix of coefficients, [X] is the vector of unknown variables, and [B] is the vector matrix of values (those on the right) of the equations. Several algorithms are available for obtaining solutions for such systems of equations, as described in Chapter 4. One of the common algorithms involves taking the inverse of the matrix of coefficients, and multiplying it by matrix [B]:

Several software programs allow execution of mathematical operations involving matrices, such as computation of a matrix inverse and matrix multiplication. The solution techniques using a spreadsheet program and Mathcad follow.
Solution (using a spreadsheet program)
The solution using Excel is shown in Figure 6.7. The first step in the solution is entering the matrix of coefficients [A] and the vector matrix of values [B]. As seen from Figure 6.7, [A] forms a 5 × 5 array occupying cells B5 through F9, while [B] is entered in cells H5 through H9. To calculate [A]-1, first a 5 × 5 space is selected—B12 through F16, as seen previously—and the matrix inverse function is entered by typing =MINVERSE(B5..F9) followed by pressing the keys <Ctrl+Shift+Enter> simultaneously. Excel calculates the inverse of the matrix and populates the cells B12 through F16 automatically. The solution to the material balance problem is then obtained by multiplying the matrices [A]-1 and [B]. This is accomplished by selecting a 5 × 1 space (H12–H16), entering the formula =MMULT(B12..B16,H5..H9), and pressing the keys <Ctrl+Shift+Enter> simultaneously. The resultant solution of the problem is seen in the cells H12 through H16, which are the values for the number of moles of CH4, CO2, CO, H2O, and O2—0.01, 0.891, 0.099, 1.98, and 0.3695, respectively.
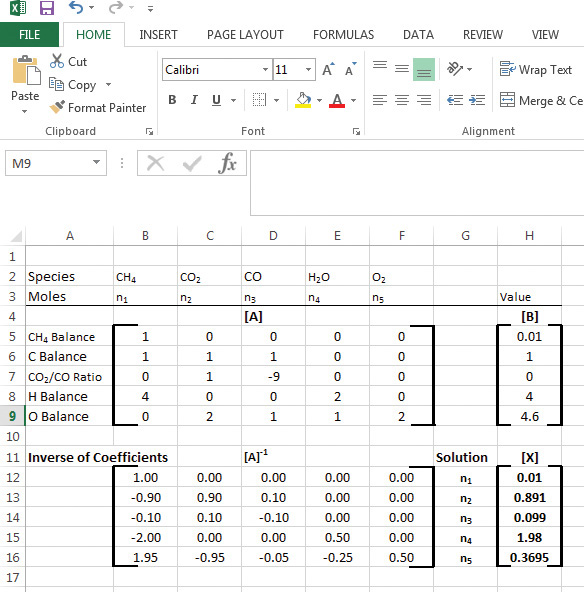
Figure 6.7 Excel solution of [A][X] = [B].
Solution (using Mathcad)
The system of linear equations [A][X] = [B] can be readily solved in Mathcad using the function lsolve([A],[B]).5 Figure 6.8 shows the Mathcad solution of the problem.
5. The algorithm used in the Mathcad lsolve function is called LU decomposition, a type of elimination algorithm mentioned in Chapter 4, the details of which are beyond the scope of this book.
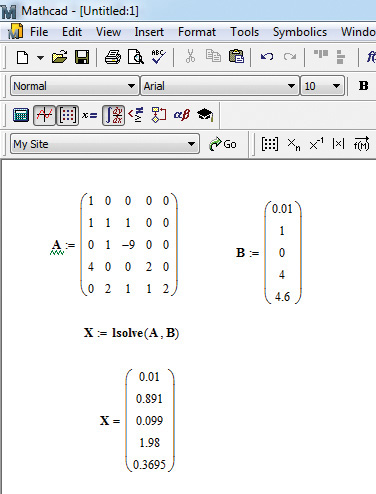
Figure 6.8 Mathcad solution of [A][X] = [B].
The calculation steps are as follows:
1. Enter the matrix coefficients by typing A:, and then either clicking on the matrix icon on the toolbar or pressing the <Ctrl+m> keys simultaneously. This brings up a dialog box; specify the number of rows and columns to be 5 each. This results in the creation of a 5 × 5 matrix with a placeholder for each matrix element. The values of the coefficients can now be entered by clicking on each placeholder.
2. Enter the matrix B using the same procedure, that is, by typing B: and pressing <Ctrl+m> or clicking on the matrix icon. The number of columns is 1 and the number of rows 5. Appropriate values are entered for each element.
3. Solve the system by typing X:lsolve(A,B).
4. Type X= results to display the solution.
Alternatively, a solution can also be obtained by entering the expression X:A-1*B. The solution is displayed by typing X=. Confirming that an identical solution is obtained is an exercise left to the reader.
As can be seen from Figures 6.6, 6.7, and 6.8, all three techniques yield identical solutions. It should be noted that it is not necessary to resort to matrix computations to solve this particular problem. The first equation readily yields the value of n1, as it involves only this variable. This value can then be substituted in other equations in appropriate sequence to solve other equations. Unfortunately, most practical systems will not yield such a convenient set of equations; however, the matrix computations illustrated here will be useful in arriving at the solution of the material balance problem.
Most practical reacting systems will involve, apart from the desired reaction, several side reactions of the primary reactant of interest. Further, the reactant mixture will inevitably contain several other constituents that undergo multiple reactions as well. The system may have multiple outlet streams in different physical states (gas, liquid, solid). It can be understood that the complexity of the system can increase significantly. Such systems cannot be solved easily through manual calculations using a basic scientific calculator (as for the system previously discussed), necessitating the use of software such as Excel or Mathcad that can rapidly solve systems containing several dozens (and possibly hundreds) of equations and variables.
Leave a Reply