Material balances in nonreacting systems are illustrated through a simple example involving dilution of a concentrated solution, an operation frequently encountered in a chemical process plant.
EXAMPLE 6.2.1 DILUTION OF A CONCENTRATED AQUEOUS SOLUTION
The production process for sodium hydroxide (NaOH) yields a 28% (by mass) solution of sodium hydroxide in a membrane cell. A subsequent process requires 1000 tons per day (tpd) of 10% NaOH solution. Calculate the quantities of the concentrated solution and diluent H2O needed to obtain this stream.
Solution
The process can be accurately represented by Figure 6.1. Let us assume that the process operates continuously at steady state, and ![]() ,
, ![]() , and
, and ![]() are the mass flow rates of the concentrated (28%) solution, diluent H2O, and dilute solution, respectively. This is a system containing two components—NaOH and H2O—and the resultant overall and component material balances are shown in equations E6.1, E6.2, and E6.3.
are the mass flow rates of the concentrated (28%) solution, diluent H2O, and dilute solution, respectively. This is a system containing two components—NaOH and H2O—and the resultant overall and component material balances are shown in equations E6.1, E6.2, and E6.3.
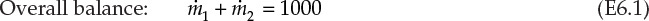
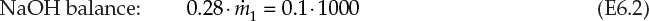
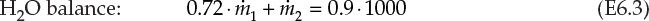
Of these three equations, only two are independent and sufficient for quantitative solution in this two-component system. The two equations to be used are the overall material balance and the component material balance for NaOH. It is preferable to use the component balance for NaOH rather than H2O, as it is present in fewer streams than is H2O. The solution steps are
1. Equation E6.2 is solved first to obtain the value of ![]() , which is 357.1 tpd.
, which is 357.1 tpd.
2. This value is substituted in equation E6.1 to obtain 642.9 tpd as the value of ![]() .
.
Therefore, 642.9 tpd of H2O needs to be added to 357.1 tpd of 28% NaOH solution to obtain 1000 tpd of the desired 10% NaOH solution. The validity of this solution can be (and should be) cross-checked with the component balance for H2O. The left side of equation E6.3 evaluated from the calculated values of ![]() and
and ![]() is found to be 900 tpd, equal to the right side of the equation.
is found to be 900 tpd, equal to the right side of the equation.
Dilution of a concentrated solution is a type of mixing operation, a common operation in chemical processes. Equally common are separation operations, which can be visualized as the inverse of mixing operations. In the simplest of separations, a single stream containing two components is separated into two streams, each with a different composition, as illustrated in example 6.2.2.
EXAMPLE 6.2.2 SEPARATION BY DISTILLATION
Distillation involves separating two or more components based on their volatilities. A 1000 kg/h stream containing 50% benzene and 50% toluene (by mass) is fed to a distillation column to obtain a benzene-rich stream at the top (distillate) and a toluene-rich stream at the bottom (bottoms). Ninety percent of the benzene fed to the column is recovered in the distillate, which has a purity of 99%. Calculate the mass and molar flow rates and compositions of both the product streams.
Solution
The schematic of this operation is shown in Figure 6.2. F, D, and B are the flow rates of the feed, distillate, and bottoms, respectively. The compositions (mass fractions) in the three streams are represented by z, y, and x, with the subscripts B and T representing benzene and toluene, respectively. The overall and component balances are shown in equations E6.4, E6.5, and E6.6.
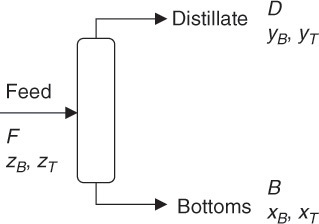
Figure 6.2 Distillation of benzene-toluene mixture.
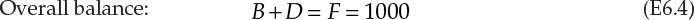
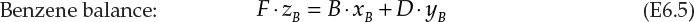
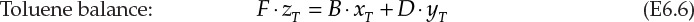
As mentioned earlier, only two of these equations are independent, with the toluene balance obtained by simply subtracting the benzene balance from the overall balance. The benzene balance can be further simplified using the information about the purity of the distillate stream. Substituting values of F, zB, and yB, in equation E6.5 reduces to the following:

To solve the system of these equations, the additional information related to the recovery of benzene must be used. Since 90% of benzene fed to the column is recovered in the distillate, the following applies:

Equation E6.8 yields the value of D to be 454.5 kg/h, which upon substitution in equation E6.4 yields B as 545.5 kg/h. The mass fraction of benzene in the bottoms, xB is then obtained from equation E6.7 to be 0.09. The mass fractions of toluene in the distillate and bottoms streams are obtained by subtracting mole fractions of benzene from 1, resulting in xT = 0.91 and yT = 0.01. The accuracy of these numbers is checked by evaluating the right side of equation E6.6:
B·xT + D·yT = 545.5×0.91 + 454.5×0.01 = 500.95 kg/h(~500 kg/h)
This calculation indicates that the values obtained by solving equations E6.4 and E6.5 satisfy equation E6.6, confirming the validity of the solution. The molar flow rates of the components can be obtained by dividing their mass flow rates by the molar masses (78 g/mol for benzene, 92 g/mol for toluene). Mole fractions of components are then obtained by dividing the molar flow rate of the component by the total molar flow rate. The resultant flow rates and compositions of various streams are shown in Tables E6.1 and E6.2, respectively.
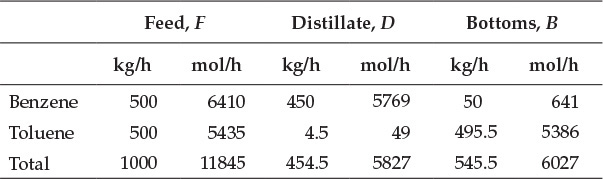
Table E6.1 Flow Rates of Streams
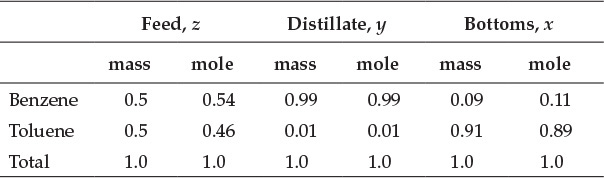
Table E6.2 Fractional Stream Compositions
These calculations can be easily performed on a basic calculator or using an appropriate software package. The Mathcad solution is shown in Figure 6.3.
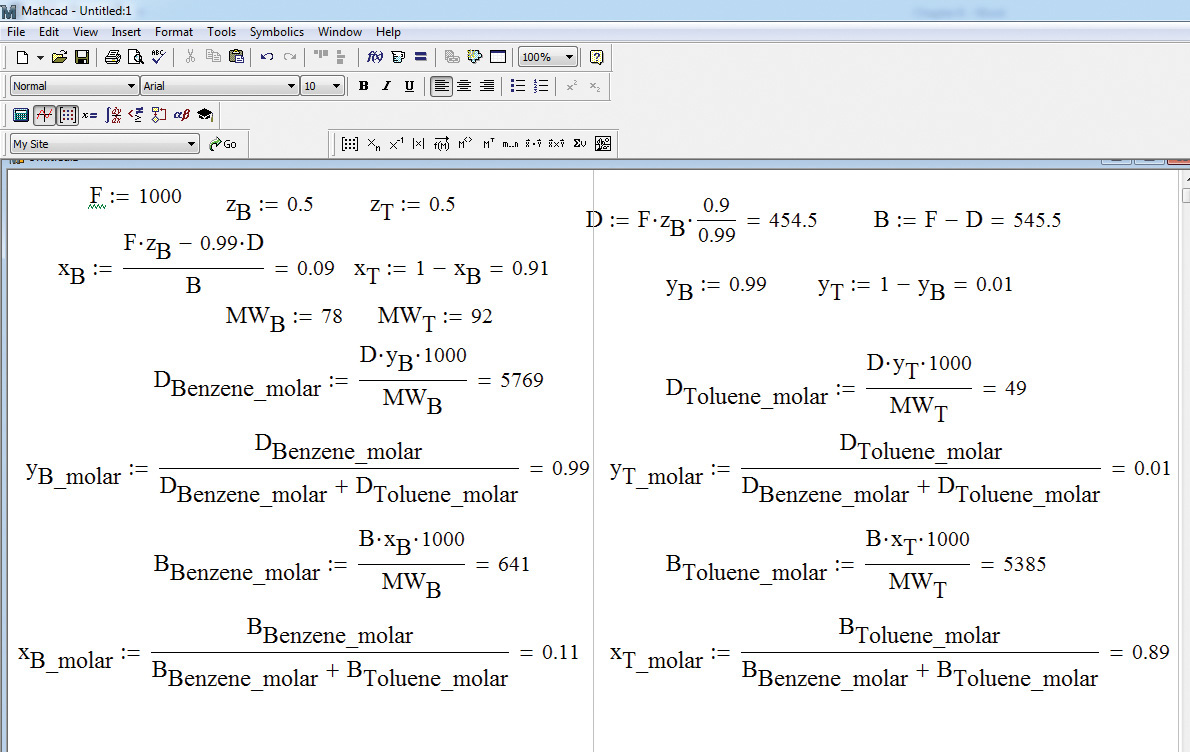
Figure 6.3 Mathcad solution of problem 6.2.2.
The benefit of using Mathcad lies in the ability to obtain the solution rapidly when the problem specifications—stream purity, component recovery, and so on—are changed. Any change in the variable is immediately reflected in the solution.
These two examples involve simple physical processes of mixing and separation. The principles and procedures used therein can readily be extended to multicomponent, multistream processes. The computations for solutions in these examples are illustrated using a mass basis; that is, quantities of various species are expressed in terms of mass units. However, for a nonreacting system, the computations can be performed equally well on a molar basis; that is, by expressing quantities of various species in terms of the number of moles present. The nonreacting systems are amenable to computations on a molar basis, as no new chemical species are created, nor any existing ones destroyed. In fact, computations using molar basis are much more common than those using a mass basis, as most relationships between chemical species are expressed typically in terms of molar concentrations. It is, of course, possible to convert these relationships on a mass basis; however, that introduces a level of complexity that is neither necessary nor desired.
Not all chemical species are conserved in a reacting system, which also involves creation of new species. The application of the overall and component material balances to chemically reacting systems involves a slightly higher level of complexity than that for a nonreacting system, as explained in the next section.
Leave a Reply