Chemical engineers require additional information (apart from the overall material balance) about material flows of components in the process and conduct component material balances over the process units. Let us assume that the process shown in Figure 6.1 is that of simple mixing of a concentrated aqueous solution of salt A (stream 1) with pure water (H2O; stream 2), yielding a dilute aqueous solution of the salt (stream 3). This is a two-component system composed of the components A and H2O. Applying the principle of the conservation of mass to each component leads to the two component balances shown in equations 6.4 and 6.5.

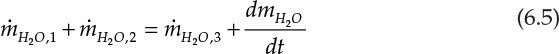
Here, mA and mH2O represent the masses of component A and H2O present in the system. Since component A is present in only one inlet stream, the left side of equation 6.4 involves only one inlet term. H2O, however, is present in both of the inlet streams, and hence, the left side of equation 6.5 has two terms. The generalized component balance equations for an n component, multistream unit can be written as follows:
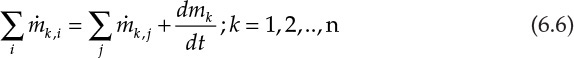
The left side of this equation represents the mass of component k being fed to the unit through all the inlet streams (summation over i inlet streams), the first term on the right side represents the mass flow rate of component k out of the system through all outlet streams (summation over j outlet streams), and the last term represents the rate of accumulation of the component mass in the system. The accumulation term will drop out of the equation for a continuous, steady-state process, simplifying the equation from a first-order ordinary differential equation to an algebraic or a transcendental equation.
In total there will be n equations representing component balances for the n components. Thus, in an n-component system, we have n independent component balance equations and one overall material balance equation—a total of n + 1 equations. However, only n of these equations are independent (distinct), as the summation of all component balances will lead to the overall material balance—equation 6.2.
The application of these principles for solving material balance problems for systems that involve only physical operations is described in section 6.2, followed by the application to reacting systems in section 6.3.
Leave a Reply