Many of the equations in chemical engineering involve functions of variables more complex than simple powers. An equation containing exponential, logarithmic, trigonometric, and other similar functions is not amenable to solution by algebraic means—that is, by simple addition, multiplication, or root extraction operations. Such equations “transcend” algebra and are called transcendental equations [4]. Equation 4.7, the Nikuradse equation, often used in fluid flow calculations, is an example of a transcendental equation [5].
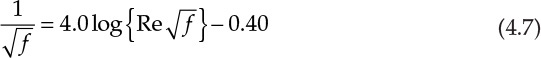
Re in the equation represents Reynolds number, a dimensionless quantity of enormous significance in fluid mechanics and transport phenomena. The Nikuradse equation allows us to calculate f, the friction factor, a quantity that further leads to the estimation of pressure drop for a flowing fluid and, ultimately, the power requirements for material transfer.
Equation 4.8 is another example of a transcendental equation that is used in the design of chemical reactors [6].

XA represents the conversion (extent of reaction) of the reactant A, τ the residence time (the time spent by the fluid in the reactor), and A and E the characteristic parameters that describe the rate of reaction. The equation can be used to calculate one of the three quantities XA, τ, or T when the other two are specified.
Many processes involve consecutive chemical reactions that can be represented by the equation A → R → S. A is the starting reactant, which upon undergoing the reaction yields the specie R, which is often the desired product. However, R may undergo further reaction forming S. The typical concentration profiles for the three species in a reactor as a function of time are shown in Figure 4.3. As can be seen, the concentration of A decreases continuously, while that of S increases continuously. The concentration of the desired product R increases first, reaches a maximum, and then starts decreasing. The concentration-time relationship for R when both the reactions are first order2 with respect to the reactants is shown in equation 4.9 [7].
2. A first-order reaction is one in which the rate of reaction is proportional to the concentration of the reactant. These concepts are presented in more detail in Chapter 9, “Computations in Chemical Engineering Kinetics.”
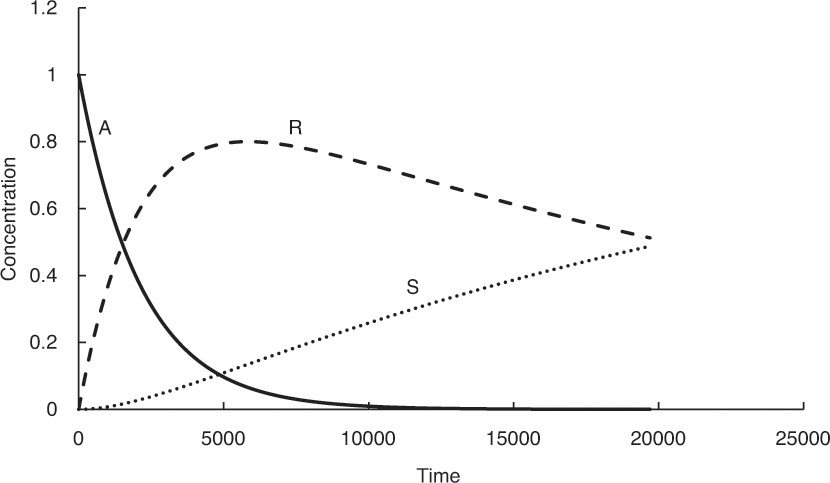
Figure 4.3 Concentration profiles of species for the consecutive reaction scheme A → R → S.
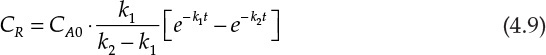
Here, CR is the concentration of R, CA0 is the initial concentration of A, and k1 and k2 are the rate constants for the two reactions. Calculating the concentration of R at any specified time, when the rate constants and initial concentration of A are known, is straightforward. However, calculation of time needed to achieve a certain specified concentration of R is more challenging and requires use of techniques needed for the solution of transcendental equations.
Leave a Reply