Interrelation between Costs

What is Cost?

Cost refers to the total expenditure made on inputs or resources that are used for the production of final goods or services. The resources used by a firm are limited in nature and thus require efficient allocation to maximise the firm’s profit. The cost or economic cost of a firm consists of all the expenses it faces, can manage, and are beyond its control.

For example, cost of labor, capital, and raw materials. Besides other resources, a firm may also use those resources whose expenses are not that clear but are still essential for the firm.

Relationship between Short-run Cost

1. Relationship between AC and MC

There is a close relationship between AC and MC.

• First of all, AC and MC both are determined from TC (Total Cost). While AC is the Total Cost (TC) per unit of output, MC is the additional TC when one more unit of output is produced.
• Secondly, because of the Law of Variable Proportion, both AC and MC curves are U-shaped.

To better understand the relationship between AC and MC, let’s take an example.

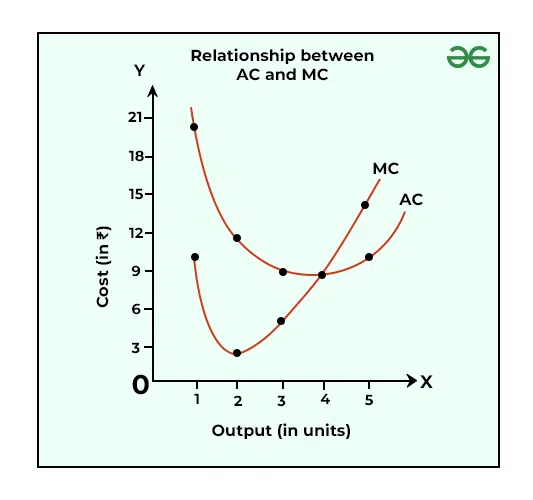
The above table and graph tell about the following relationship between AC and MC:

1. When MC is less than AC, AC falls with an increase in output. It happens till 3 units of output.
2. When MC is equal to AC; i.e., when the MC and AC curve intersect each other at A, AC is constant and is also at its minimum. It happens at 4 units of output.
3. When MC is greater than AC, AC increases with an increase in output. It happens from 5 units of output.

Besides, AC and MC both increase, but, as compared to AC, MC increases at a faster rate. Therefore, the MC curve is steeper than the AC curve.

AC depends on the nature of MC

Among AC and MC, MC is responsible for the changes in AC. It means that, when MC falls, it also pulls down AC, and when MC rises, it pulls up AC. Simply put,

• When MC curve lies below the AC curve, it pulls the AC curve downwards.
• When MC curve intersects the AC curve, both are equal.
• When MC curve lies above the AC curve, it pulls the AC curve upwards.

Is it possible for AC to fall, when MC is rising?

Yes, it is possible for AC to fall, when MC is rising. It can happen only when MC is less than AC. In simple terms, as long as the MC curve is below the AC curve, AC will continue to fall even if MC is rising. In the above example, when we move from 2 units to 3 units, even though AC falls, MC keeps on rising because at these points MC < AC.

Is it possible for AC to rise, when MC is falling?

No, it is not possible for AC to rise, when MC is falling because when MC falls, AC also falls.

2. Relationship between AVC and MC

The relationship between AVC and MC is quite similar to the relationship between AC and MC in the following ways:

• First of all, AVC and MC both are determined from TVC (Total Variable Cost). While AVC is the Total Variable Cost (TVC) per unit of output, MC is the additional TC when one more unit of output is produced.
• Secondly, because of the Law of Variable Proportion, both AVC and MC curves are U-shaped.

To better understand the relationship between AVC and MC, let’s take an example.

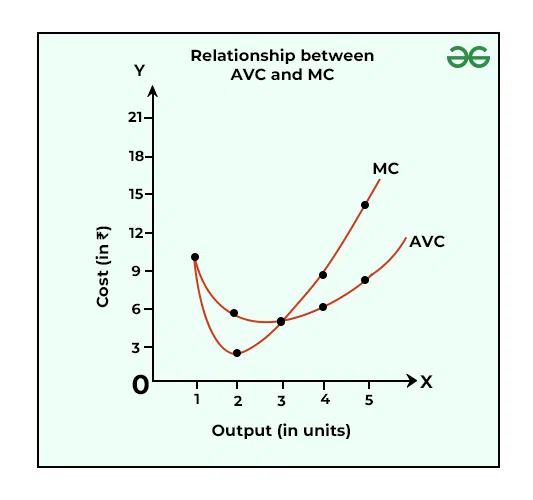
The above table and graph tell about the following relationship between AVC and MC:

1. When MC is less than AVC, AVC falls with an increase in output. It happens until 2 units of output.
2. When MC is equal to AVC; i.e., when MC and AVC curves intersect each other at B, AVC is constant and is also at its minimum. It happens at 3 units of output.
3. When MC is greater than AVC, AVC increases with an increase in output. It happens from 4 units of output.

Besides, AVC and MC both increase, but, as compared to AVC, MC increases at a faster rate. Therefore, the MC curve is steeper than the AVC curve.

3. Relationship between AC, AVC, and MC

To better understand the relationship between AC, AVC, and MC, let’s take an example:

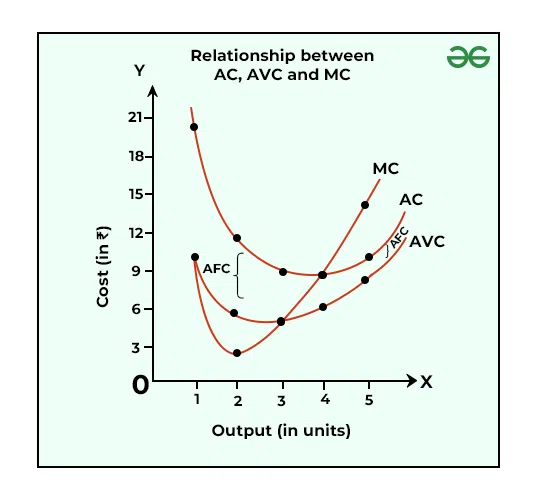
The above table and graph tell about the following relationship between AC, AVC, and MC:

1. When MC is less than both AC and AVC, they both fall with an increase in the output.
2. When MC becomes equal to AC and AVC, both become constant. The MC curve cuts the AC curve at point A and the AVC curve at point B at their minimum points.
3. When MC is more than both AC and AVC, both of them rise with an increase in output.

4. Relationship between AC and AVC

The relationship between AC and AVC is as follows:

1. AC is greater than AVC, and the amount of increment is equal to AFC.
2. With an increase in the output, the vertical distance between the AC curve and AVC curve continues to fall. It is because of the gap between them which is equal to AFC and continues to decline with an increase in output.
3. As AFC can never be zero, AC and AVC curves never intersect each other.
4. Because of the Law of Variable Proportions, both AC curve and AVC curve are U-shaped.
5. AVC and AC curves are cut by MC curve at their minimum points.
6. The minimum point of the AC curve; i.e., point A, always lies to the right of the minimum point of the AVC curve; i.e., point B.

5. Relationship between TC and MC

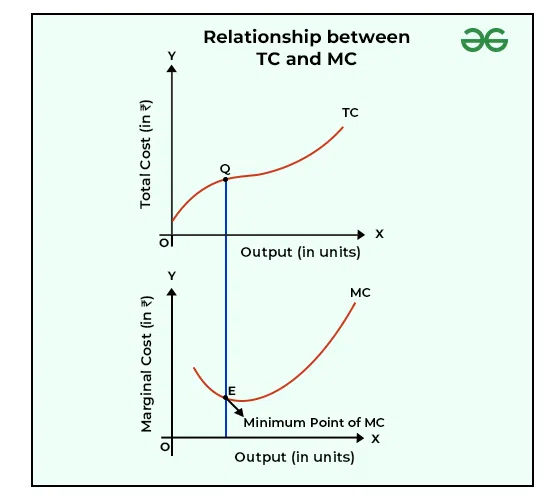
The relationship between TC and MC is as follows:

1. MC is the additional TC when one more unit of output is produced. The formula for calculating MC is TC_n – TC_n-1.
2. When TC increases at a decreasing rate; i.e., up to point Q in the above diagram, MC declines.
3. At point Q, the Total Cost stops rising at a declining rate. It is because MC is at its minimum; i.e., point E.
4. After point Q, the Total Cost starts increasing at an increasing rate. It is because now MC is rising.

6. Relationship between TVC and MC

As we already know, MC is the additional TC when one more unit of output is produced. Therefore, TVC can be determined by adding MC’s of all the units produced. Besides, if it is assumed that the output is perfectly divisible, then the total area under the MC curve will be the same as TVC.

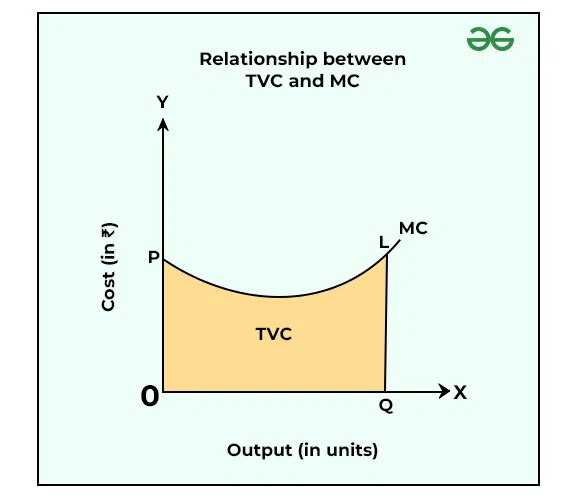
In the above diagram, it can be seen that at OQ output level, the Total Variable Cost is equal to the shaded area OQLP.