What is Consumer’s Equilibrium?
The term equilibrium is used frequently in economic analysis. It is a state of rest or a position of no change, which under a situation provides the maximum gain. A consumer is said to be in equilibrium when he has derived maximum satisfaction and does not want to change his consumption level. Hence, Consumer’s Equilibrium is a situation in which a consumer has maximum satisfaction with limited income and does not tend to change his existing way of expenditure.
As a consumer has to pay for each unit of commodity, he cannot purchase or consume unlimited quantities. Besides, according to the Law of Diminishing Marginal Utility, as the consumer consumes an additional unit of a commodity, the utility derived from the same decreases. Also, by purchasing more units of a commodity, the income of the consumer decreases. Therefore, the aim of a rational consumer is to balance his expenditure in a way that he gets maximum satisfaction by spending a minimum amount of income, and when the consumer successfully accomplishes his aim, he is said to be in equilibrium.
Two different situations in which Consumer’s Equilibrium can be studied are:
- When a consumer spends his entire income on a Single Commodity
- When a consumer spends his entire income on Two Commodities
Consumer’s Equilibrium in Single Commodity Case
Consumer’s Equilibrium in the case of a single commodity can be explained with the help of the Law of Diminishing Marginal Utility. Hence, to study the case of a single commodity, all the assumptions of the Law of DMU are considered in this study. A consumer purchasing a single commodity will be at equilibrium when he buys the commodity in such a quantity that gives him maximum satisfaction. Besides, the two factors which affect the number of units of the given commodity to be consumed are the Price of the given commodity and the Marginal Utility from each successive unit. In order to determine the equilibrium point, the consumer compares the price of the given commodity with the satisfaction level derived from it (utility). Being a rational consumer, he will be at an equilibrium level when the price paid for the commodity is equal to marginal utility.
Now, we know that Marginal Utility is measured in utils and the price is expressed in rupees; therefore, to determine the equilibrium level it is essential to express MU in terms of money, as:
Formula
�������� ������� �� ����� �� �����=�������� ������� �� ������������� ������� �� ��� ����� (���)Marginal Utility in terms of Money=Marginal Utility of one rupee (MUM)Marginal Utility in Utils
Marginal Utility of one rupee is the extra utility obtained when an additional rupee is spent on other goods.
Besides, utility differs from one person to another as it is a subjective concept. Under the single commodity case, it is assumed that a consumer defines the Marginal Utility of one rupee himself, in terms of satisfaction from the given bundle of goods.
Equilibrium Condition under Single Commodity
A consumer, when consuming a single commodity (say x) will be at equilibrium when: Marginal Utility (MUx) is equal to Price (Px) paid for the commodity.
MUx = Px
If MUx > Px, then the consumer will not be at equilibrium and he continues to purchase the commodity as the benefit gained from the consumption is more than the cost of the commodity. As the consumer buys more, Marginal Utility falls because of the Law of DMU, and when it becomes equal to the price, the consumer gets maximum satisfaction and is said to be in equilibrium.
Similarly, if MUx < Px, then also the consumer will not be at equilibrium and he will have to reduce the consumption of the commodity in order to increase the satisfaction level, till MU becomes equal to the price.
For example:
Let’s assume, a consumer wants to buy a good (say x), of price ₹10 per unit and the marginal utility derived from each successive unit (in utils and in ₹) is as follows (let’s assume that 1 util/MUM = ₹1):
| Units of x | Price (Px) (₹) | Marginal Utility (Utils) | Marginal Utility in ₹ (MUx) 1 util = ₹1 | MUx – Px | Remarks |
|---|---|---|---|---|---|
| 1 | 10 | 30 | 30/1 = 30 | 20 | Here, MUx > Px, so the consumer will increase the consumption |
| 2 | 10 | 20 | 20/1 = 20 | 10 | |
| 3 | 10 | 10 | 10/1 = 10 | 0 | Consumer’s Equilibrium MUx = Px |
| 4 | 10 | 0 | 0/1 = 0 | -10 | Here, MUx < Px, so the consumer will decrease the consumption |
| 5 | 10 | -10 | -10/1 = -10 | -20 |
This result can be shown with the help of a diagram.
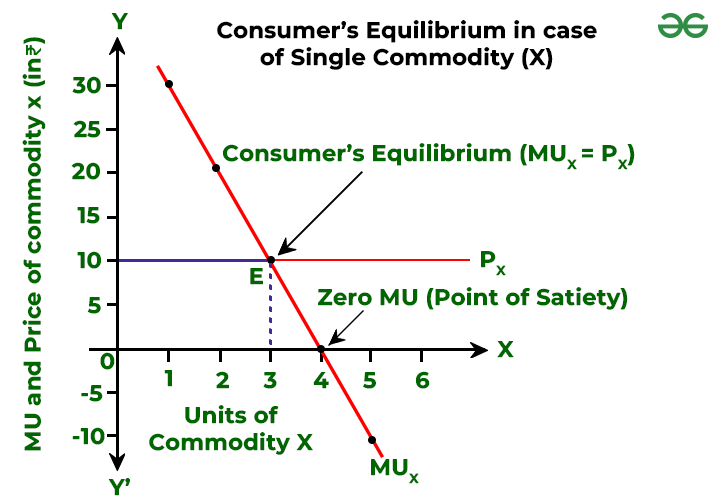
In the above graph, the slope of the curve is going downward, which indicates that the marginal utility falls when an additional commodity of x is consumed (because of the Law of DMU). Also, the Price (Px) is a straight horizontal line as the price of the commodity is fixed at ₹10 per unit.
With the help of the above schedule and graph, it can be said that the consumer will be at equilibrium at point E, when he consumes 3 units of commodity x because at that point MUx = Px.
The consumer will not consume 4 units of the commodity x because the MU of ₹0 is less than the price paid for x; i.e., ₹10. Similarly, he will not consume 2 units of the commodity x because the MU of ₹20 is more than the price paid for x; i.e., ₹10.
Hence, in conclusion, it can be said that a consumer consuming a single commodity (say x) will be at equilibrium when the Marginal Utility from the commodity (MUx) is equal to the price paid for the commodity (Px).
The equilibrium condition in the case of a single commodity can be expressed as:
������=��MUMMUx=Px
, or �����=���PxMUx=MUM
Consumer’s Equilibrium in Two Commodities Case
The Law of Diminishing Marginal Utility is applicable only in the case of either one commodity or single use of a commodity. However, in reality, consumers consume more than one commodity; therefore, in those cases, the Law of Equi-Marginal Utility is used as it helps in the optimum allocation of the consumer’s income.
Law of Equi-Marginal Utility also known as the Law of Substitution, Law of Maximum Satisfaction, and Gossen’s Second Law is based on the Law of DMU; therefore, all of its assumptions will apply to the Law of Equi-Marginal Utility also. The Law of Equi-Marginal Utility, states that a consumer gets maximum satisfaction, when ratios of MU of two commodities and their respective prices are equal and MU falls as consumption increases.
Let’s take an example to understand this concept. Suppose, there are two commodities x and y upon which the consumer wants to allocate his income to attain the equilibrium position. The consumer will be at equilibrium when the MU of commodities x and y will be equal to their respective prices.
Two necessary conditions to attain Consumer’s Equilibrium in Two Commodities Case
1. Ratio of Marginal Utility to Price is the same in the case of both goods (x and y):
We already know that a consumer consuming a single commodity (say x) will be at equilibrium when �����=��� PxMUx=MUM ………………….(1)
Similarly, a consumer consuming another commodity (say y) will be at equilibrium when �����=��� PyMUy=MUM ………………………(2)
By Equating (1) and (2), we get ����������=���PxMUxPyMUy=MUM
As we assume that the Marginal Utility of Money (MUM) is constant, the above equilibrium condition can be restated as:
�����=����� PxMUx=PyMUy , or ������=����MUyMUx=PyPx
When Px = Py then the equilibrium condition can be written as MUx = MUy.
2. MU falls as consumption increases:
Another condition required for attaining consumer’s equilibrium in two commodities cases is that the MU of a commodity must fall as more of it is consumed by the consumer. If the MU of a commodity does not fall with an increase in its consumption, then the consumer will continue to buy that one commodity only, which does not happen in reality, and the consumer will never reach at the equilibrium position.
Finally, it can be said that a consumer consuming two commodities will be at equilibrium when he spends his income in a way that the ratios of Marginal Utilities of two commodities and their respective prices are equal, and as the consumption increases MU falls.
When ����� PxMUx is not equal to �����PyMUy
- If �����>����� PxMUx>PyMUy , it means that the consumer is getting more Marginal Utility from commodity x as compared to commodity y. Therefore, the consumer will purchase more of x and less of y, resulting in a fall in MUx and increase in MUy. The consumer will continue to purchase more of x till, �����=�����PxMUx=PyMUy
- If �����<����� PxMUx<PyMUy , it means that the consumer is getting more Marginal Utility from commodity y as compared to commodity x. Therefore, the consumer will purchase more of y and less of x, resulting in a fall in MUy and increase in MUx. The consumer will continue to purchase more of y till �����=�����PxMUx=PyMUy
For example:
Let us assume that the total money income of a consumer is ₹7, which he wants to spend on commodities x and y. The price of each of these commodities is ₹1 per unit. Hence, the consumer can purchase maximum 7 units of commodity x, or 7 units of commodity y. The marginal utility derived by the consumer from different units of x and y are:
| Units | MU of Commodity x (in utils) | MU of commodity y (in utils) |
|---|---|---|
| 1 | 26 | 22 |
| 2 | 20 | 18 |
| 3 | 16 | 15 |
| 4 | 15 | 13 |
| 5 | 12 | 11 |
| 6 | 10 | 4 |
| 7 | 4 | 2 |
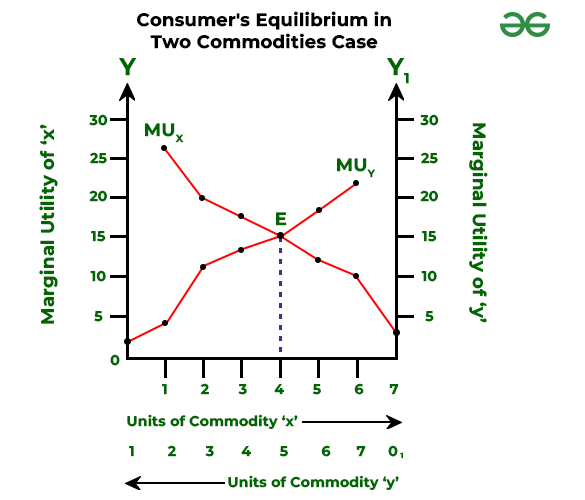
In the above graph, MU for commodity x is represented on OY-axis, and MU from commodity y is represented on O1Y1-axis. Besides, MUx and MUy are the Marginal Utility curves for commodities x and y, respectively.
The above table and graph clearly show that the consumer will spend the first rupee on commodity x, which will provide him 26 utils of utility and will spend the second rupee on commodity y which will provide him 22 utils of utility. In order to reach the position of equilibrium, the consumer should buy that combination of goods x and y, when the MU of the last rupee spent on each commodity (x and y) is the same and MU falls as consumption increases.
Both these conditions meet at point E when the consumer purchases 4 units of commodity x and 3 units of commodity y.
Now, the consumer attains equal marginal utility while consuming 7 units of commodity x and 6 units of commodity y; but the equilibrium will not be reached at this combination because the total satisfaction obtained from this combination is 52 utils [(7×4)+(6×4)]; however, total satisfaction obtained from combination at point E is 105 utils [(15×4)+(15×3)]. It means that if the consumer spends his income on any other combination other than 4 units of commodity x and 3 units of commodity y, the total satisfaction will be less than 105 utils.
Leave a Reply