We next examine the work done on an object by the gravitational force acting on it. Figure 7-6 shows a particle-like tomato of mass m that is thrown upward with initial speed v0 and thus with initial kinetic energy 
. As the tomato rises, it is slowed by a gravitational force 
; that is, the tomato’s kinetic energy decreases because does work on the tomato as it rises.
Because we can treat the tomato as a particle, we can use Eq. 7-7 (W = Fd cos 
) to express the work done during a displacement 
. For the force magnitude F, we use mg as the magnitude of . Thus, the work Wg done by the gravitational force is
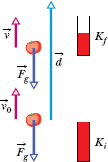
Fig. 7-6 Because the gravitational force acts on it, a particle-like tomato of mass m thrown upward slows from velocity 
to velocity 
during displacement . A kinetic energy gauge indicates the resulting change in the kinetic energy of the tomato, from to Kf 
.
For a rising object, force is directed opposite the displacement , as indicated in Fig. 7-6. Thus, = 180° and
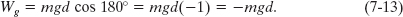
The minus sign tells us that during the object’s rise, the gravitational force acting on the object transfers energy in the amount mgd from the kinetic energy of the object. This is consistent with the slowing of the object as it rises.
After the object has reached its maximum height and is falling back down, the angle between force and displacement is zero. Thus,
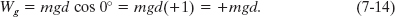
The plus sign tells us that the gravitational force now transfers energy in the amount mgd to the kinetic energy of the object. This is consistent with the speeding up of the object as it falls. (Actually, as we shall see in Chapter 8, energy transfers associated with lifting and lowering an object involve not just the object, but the full object–Earth system. Without Earth, of course, “lifting” would be meaningless.)
Work Done in Lifting and Lowering an Object
Now suppose we lift a particle-like object by applying a vertical force 
to it. During the upward displacement, our applied force does positive work Wa on the object while the gravitational force does negative work Wg on it. Our applied force tends to transfer energy to the object while the gravitational force tends to transfer energy from it. By Eq. 7-10, the change Δ K in the kinetic energy of the object due to these two energy transfers is
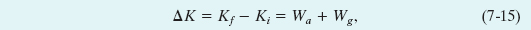
in which Kf is the kinetic energy at the end of the displacement and Ki is that at the start of the displacement. This equation also applies if we lower the object, but then the gravitational force tends to transfer energy to the object while our force tends to transfer energy from it.
In one common situation, the object is stationary before and after the lift—for example, when you lift a book from the floor to a shelf. Then Kf and Ki are both zero, and Eq. 7-15 reduces to
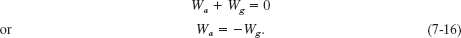
Note that we get the same result if Kf and Ki are not zero but are still equal. Either way, the result means that the work done by the applied force is the negative of the work done by the gravitational force; that is, the applied force transfers the same amount of energy to the object as the gravitational force transfers from the object. Using Eq. 7-12, we can rewrite Eq. 7-16 as
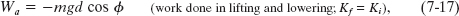
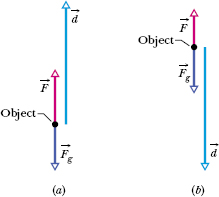
Fig. 7-7 (a) An applied force lifts an object. The object’s displacement makes an angle = 180° with the gravitational force on the object. The applied force does positive work on the object. (b) An applied force lowers an object. The displacement of the object makes an angle = 0° with the gravitational force . The applied force does negative work on the object.
with being the angle between and . If the displacement is vertically upward (Fig. 7-7a), then = 180° and the work done by the applied force equals mgd. If the displacement is vertically downward (Fig. 7-7b), then = 0° and the work done by the applied force equals −mgd.
Equations 7-16 and 7-17 apply to any situation in which an object is lifted or lowered, with the object stationary before and after the lift. They are independent of the magnitude of the force used. For example, if you lift a mug from the floor to over your head, your force on the mug varies considerably during the lift. Still, because the mug is stationary before and after the lift, the work your force does on the mug is given by Eqs. 7-16 and 7-17, where, in Eq. 7-17, mg is the weight of the mug and d is the distance you lift it.
In the 1950s, Paul Anderson (Fig. 7-8) became legendary for lifting tremendous loads. One of his lifts remains a record: Anderson stooped beneath a reinforced wood platform, placed his hands on a short stool to brace himself, and then pushed upward on the platform with his back, lifting the platform straight up a distance of about 1.0 cm. The platform held automobile parts and a safe filled with lead, with a total weight of 27 900 N (6270 lb).
(a) As Anderson lifted the load, how much work was done on it by the gravitational force ?
Solution: The Key Idea here is that we can treat the load as a single particle because the components moved rigidly together. Thus we can use Eq. 7-12 (W = mgd cos ) to find the work Wg done on the load by . The angle between the directions of the downward gravitational force and the upward displacement was 180°. Substituting this and the given data into Eq. 7-12, we find
Fig. 7-8 Using a harness across his back, Paul Anderson lifted a platform and a scout troop off the ground.
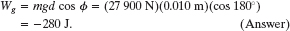
(b) How much work was done by the force Anderson applied to make the lift?
Solution: We do not have an expression for Anderson’s force on the load, and even if we did, his force was certainly not constant. Thus, one Key Idea here is that we cannot just substitute the force magnitude into Eq. 7-7 to find the work done. However, we know that the load was stationary both at the start and at the end of the lift. Therefore, as a second Key Idea, we know that the work WA done by Anderson’s applied force was the negative of the work Wg done by the gravitational force . Equation 7-16 expresses this fact and gives us
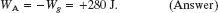
This is hardly more than the work needed to lift a stuffed school backpack from the floor to shoulder level. So, why was Anderson’s lift so amazing? Work (energy transfer) and force are different quantities; although Anderson’s lift required an unremarkable energy transfer, it required a truly remarkable force.
An initially stationary 15.0 kg crate of cheese wheels is pulled, via a cable, a distance d = 5.70 m up a frictionless ramp to a height h of 2.50 m, where it stops (Fig. 7-9a).
(a) How much work Wg is done on the crate by the gravitational force during the lift?
Solution: A Key Idea is that we can treat the crate as a particle and thus use Eq. 7-12 (Wg = mgd cos ) to find the work Wg done by . However, we do not know the angle between the directions of and displacement . From the crate’s free-body diagram in Fig. 7-9b, we find that is θ + 90°, where θ is the (unknown) angle of the ramp. Equation 7-12 then gives us
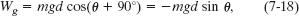
where we have used a trigonometic identity to simplify the expression. The result seems to be useless because θ is unknown. But (continuing with physics courage) we see from Fig. 7-9a that d sin θ = h, where h is a known quantity. With this substitution, Eq. 7-18 gives us
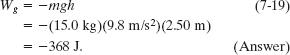
Note that Eq. 7-19 tells us that the work Wg done by the gravitational force depends on the vertical displacement but (surprisingly) not on the horizontal displacement. (We return to this point in Chapter 8.)
(b) How much work WT is done on the crate by the force 
from the cable during the lift?
Solution: We cannot just substitute the force magnitude T for F in Eq. 7-7 (W = Fd cos ) because we do not know the value of T. However, a Key Idea to get us going is that we can treat the crate as a particle and then apply the work–kinetic energy theorem (Δ K = W) to it. Because the crate is stationary before and after the lift, the change Δ K in its kinetic energy is zero. For the net work W done on the crate, we must sum the works done by all three forces acting on the crate. From (a), the work Wg done by the gravitational force is −368 J. The work WN done by the normal force 
on the crate from the ramp is zero because is perpendicular to the displacement. We want the work WT done by . Thus, the work–kinetic energy theorem gives us
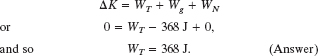
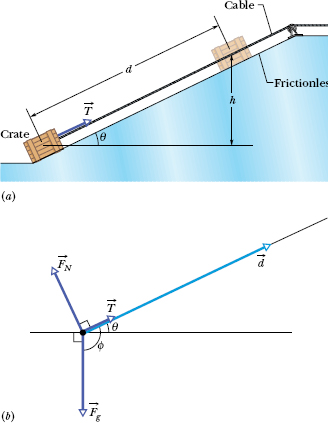
Fig. 7-9 (a) A crate is pulled up a frictionless ramp by a force parallel to the ramp. (b) A free-body diagram for the crate, showing also the displacement .
CHECK POINT 3 Suppose we raise the crate by the same height h but with a longer ramp. (a) Is the work done by force now greater than, smaller than, or the same as before? (b) Is the magnitude of needed to move the crate now greater than, smaller than, or the same as before?
An elevator cab of mass m = 500 kg is descending with speed v = 4.0 m/s when its supporting cable begins to slip, allowing it to fall with constant acceleration 
(Fig. 7-10a).
(a) During the fall through a distance d = 12 m, what is the work Wg done on the cab by the gravitational force ?
Solution: The Key Idea here is that we can treat the cab as a particle and thus use Eq. 7-12 (Wg = mgd cos ) to find the work Wg done on it by . From Fig. 7-10b, we see that the angle between the directions of and the cab’s displacement is 0°. Then, from Eq. 7-12, we find
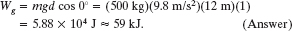
(b) During the 12 m fall, what is the work WT done on the cab by the upward pull of the elevator cable?
Solution: A Key Idea here is that we can calculate the work WT with Eq. 7-7 (W = Fd cos ) if we first find an expression for the magnitude T of the cable’s pull. A second Key Idea is that we can find that expression by writing Newton’s second law for components along the y axis in Fig. 7-10b (Fnet,y = may). We get
T − Fg = ma.
Solving for T, substituting mg for Fg, and then substituting the result in Eq. 7-7, we obtain
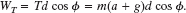
Next, substituting −g/5 for the (downward) acceleration a and then 180° for the angle between the directions of forces and 
, we find
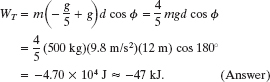
Note that WT is not simply the negative of Wg. The reason is that, because the cab accelerates during the fall, its speed changes during the fall, and thus its kinetic energy also changes. Therefore, Eq. 7-16 (which assumes that the initial and final kinetic energies are equal) does not apply here.
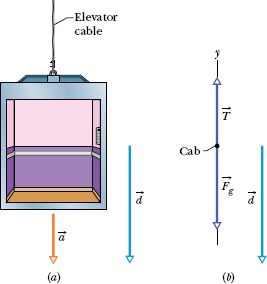
Fig. 7-10 An elevator cab, descending with speed vi, suddenly begins to accelerate downward. (a) It moves through a displacement with constant acceleration . (b) A free-body diagram for the cab, displacement included.
(c) What is the net work W done on the cab during the fall?
Solution: The Key Idea here is that the net work is the sum of the works done by the forces acting on the cab:
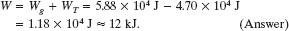
(d) What is the cab’s kinetic energy at the end of the 12 m fall?
Solution: The Key Idea here is that the kinetic energy changes because of the net work done on the cab, according to Eq. 7-11 (Kf = Ki + W). From Eq. 7-1, we can write the kinetic energy at the start of the fall as 
. We can then write Eq. 7-11 as
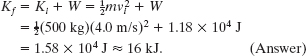
Leave a Reply