Work and Kinetic Energy

Finding an Expression for Work

Let us find an expression for work by considering a bead that can slide along a frictionless wire that is stretched along a horizontal x axis (Fig. 7-2). A constant force , directed at an angle  to the wire, accelerates the bead along the wire. We can relate the force and the acceleration with Newton’s second law, written for components along the x axis:

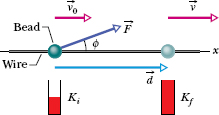
Fig. 7-2   A constant force  directed at angle  to the displacement  of a bead on a wire accelerates the bead along the wire, changing the velocity of the bead from  to . A “kinetic energy gauge” indicates the resulting change in the kinetic energy of the bead, from the value K_i to the value K_f.

where m is the bead’s mass. As the bead moves through a displacement , the force changes the bead’s velocity from an initial value  to some other value . Because the force is constant, we know that the acceleration is also constant. Thus, we can use Eq. 2-16 to write, for components along the x axis,

Solving this equation for a_x, substituting into Eq. 7-3, and rearranging then give us

The first term on the left side of the equation is the kinetic energy K of the bead at the end of the displacement d, and the second term is the kinetic energy K_i of the bead at the start of the displacement. Thus, the left side of Eq. 7-5 tells us the kinetic energy has been changed by the force, and the right side tells us the change is equal to F_xd. Therefore, the work W done on the bead by the force (the energy transfer due to the force) is

If we know values for F_x and d, we can use this equation to calculate the work W done on the bead by the force.

To calculate the work a force does on an object as the object moves through some displacement, we use only the force component along the object’s displacement. The force component perpendicular to the displacement does zero work.

From Fig. 7-2, we see that we can write F_x as F cos , where  is the angle between the directions of the displacement  and the force . We can rewrite Eq. 7-6 in a more general form as

This equation is useful for calculating the work if we know values for F, d, and . Because the right side of this equation is equivalent to the scalar (dot) product  · , we can also write

where F is the magnitude of . (You may wish to review the discussion of scalar products in Section 3-8.) Equation 7-8 is especially useful for calculating the work when  and  are given in unit-vector notation.

Cautions: There are two restrictions to using Eqs. 7-6 through 7-8 to calculate work done on an object by a force. First, the force must be a constant force; that is, it must not change in magnitude or direction as the object moves. (Later, we shall discuss what to do with a variable force that changes in magnitude.) Second, the object must be particle-like. This means that the object must be rigid; all parts of it must move together, in the same direction. In this chapter we consider only particle-like objects, such as the bed and its occupant being pushed in Fig. 7-3.

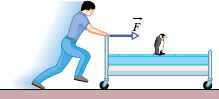
Fig. 7-3   A contestant in a bed race. We can approximate the bed and its occupant as being a particle for the purpose of calculating the work done on them by the force applied by the student.

Signs for work. The work done on an object by a force can be either positive work or negative work. For example, if the angle  in Eq. 7-7 is less than 90°, then cos  is positive and thus so is the work. If  is greater than 90° (up to 180°), then cos  is negative and thus so is the work. (Can you see that the work is zero when  = 90°?) These results lead to a simple rule. To find the sign of the work done by a force, consider the force vector component that is parallel to the displacement:

A force does positive work when it has a vector component in the same direction as the displacement, and it does negative work when it has a vector component in the opposite direction. It does zero work when it has no such vector component.

Units for work. Work has the SI unit of the joule, the same as kinetic energy. However, from Eqs. 7-6 and 7-7 we can see that an equivalent unit is the newton-meter (N · m). The corresponding unit in the British system is the foot-pound (ft · lb). Extending Eq. 7-2, we have

Net work done by several forces. When two or more forces act on an object, the net work done on the object is the sum of the works done by the individual forces. We can calculate the net work in two ways. (1) We can find the work done by each force and then sum those works. (2) Alternatively, we can first find the net force _net of those forces. Then we can use Eq. 7-7, substituting the magnitude F_net for F and also the angle between the directions of _net and  for . Similarly, we can use Eq. 7-8 with _net substituted for .

Work–Kinetic Energy Theorem

Equation 7-5 relates the change in kinetic energy of the bead (from an initial  to a later ) to the work W (= F_xd) done on the bead. For such particle-like objects, we can generalize that equation. Let Δ K be the change in the kinetic energy of the object, and let W be the net work done on it. Then we can write

which says that

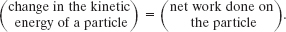
We can also write

which says that

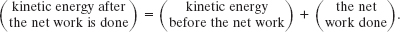
These statements are known traditionally as the work–kinetic energy theorem for particles. They hold for both positive and negative work: If the net work done on a particle is positive, then the particle’s kinetic energy increases by the amount of the work. If the net work done is negative, then the particle’s kinetic energy decreases by the amount of the work.

For example, if the kinetic energy of a particle is initially 5 J and there is a net transfer of 2 J to the particle (positive net work), the final kinetic energy is 7 J. If, instead, there is a net transfer of 2 J from the particle (negative net work), the final kinetic energy is 3 J.

 CHECK POINT 1 A particle moves along an x axis. Does the kinetic energy of the particle increase, decrease, or remain the same if the particle’s velocity changes (a) from −3 m/s to −2 m/s and (b) from −2 m/s to 2 m/s? (c) In each situation, is the work done on the particle positive, negative, or zero?

Sample Problem 7-2

Figure 7-4a shows two industrial spies sliding an initially stationary 225 kg floor safe a displacement  of magnitude 8.50 m, straight toward their truck. The push  of spy 001 is 12.0 N, directed at an angle of 30.0° downward from the horizontal; the pull  of spy 002 is 10.0 N, directed at 40.0° above the horizontal. The magnitudes and directions of these forces do not change as the safe moves, and the floor and safe make frictionless contact.

(a) What is the net work done on the safe by forces  and  during the displacement ?

Solution: We use two Key Ideas here. First, the net work W done on the safe by the two forces is the sum of the works they do individually. Second, because we can treat the safe as a particle and the forces are constant in both magnitude and direction, we can use either Eq. 7-7 (W = Fd cos ) or Eq. 7-8 (W =  · ) to calculate those works. Since we know the magnitudes and directions of the forces, we choose Eq. 7-7. From it and the free-body diagram for the safe in Fig. 7-4b, the work done by  is

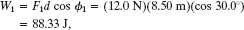
and the work done by  is

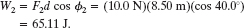
Thus, the net work W is

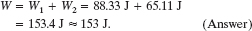
During the 8.50 m displacement, therefore, the spies transfer 153 J of energy to the kinetic energy of the safe.

(b) During the displacement, what is the work W_g done on the safe by the gravitational force  and what is the work W_N done on the safe by the normal force  from the floor?

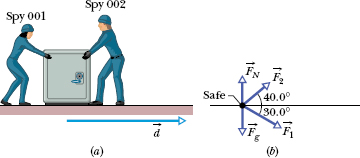
Fig. 7-4   (a) Two spies move a floor safe through a displacement . (b) A free-body diagram for the safe.

Solution: The Key Idea is that, because these forces are constant in both magnitude and direction, we can find the work they do with Eq. 7-7. Thus, with mg as the magnitude of the gravitational force, we write

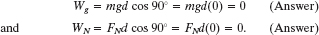
We should have known this result. Because these forces are perpendicular to the displacement of the safe, they do zero work on the safe and do not transfer any energy to or from it.

(c) The safe is initially stationary. What is its speed v_f at the end of the 8.50 m displacement?

Solution: Here the Key Idea is that the speed of the safe changes because its kinetic energy is changed when energy is transferred to it by  and . We relate the speed to the work done by combining Eqs. 7-10 and 7-1:

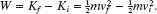
The initial speed v_i is zero, and we now know that the work done is 153.4 J. Solving for v_f and then substituting known data, we find that

Sample Problem 7-3

During a storm, a crate of crepe is sliding across a slick, oily parking lot through a displacement  while a steady wind pushes against the crate with a force . The situation and coordinate axes are shown in Fig. 7-5.

(a) How much work does this force do on the crate during the displacement?

Solution: The Key Idea here is that, because we can treat the crate as a particle and because the wind force is constant (“steady”) in both magnitude and direction during the displacement, we can use either Eq. 7-7 (W = Fd cos ) or Eq. 7-8 (W =  · ) to calculate the work. Since we know  and  in unit-vector notation, we choose Eq. 7-8 and write

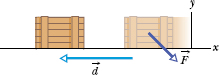
Fig. 7-5   A constant force  slows a crate during displacement .

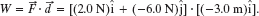
Of the possible unit-vector dot products, only , and  are nonzero (see Appendix E). Here we obtain

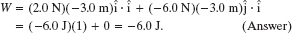
Thus, the force does a negative 6.0 J of work on the crate, transferring 6.0 J of energy from the kinetic energy of the crate.

(b) If the crate has a kinetic energy of 10 J at the beginning of displacement , what is its kinetic energy at the end of ?

Solution: The Key Idea here is that, because the force does negative work on the crate, it reduces the crate’s kinetic energy. Using the work–kinetic energy theorem in the form of Eq. 7-11, we have

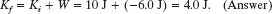
Because the kinetic energy is decreased to 4.0 J, the crate has been slowed.

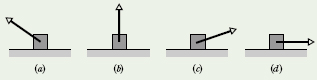
 CHECK POINT 2 The figure shows four situations in which a force acts on a box while the box slides rightward a distance d across a frictionless floor. The magnitudes of the forces are identical; their orientations are as shown. Rank the situations according to the work done on the box during the displacement, most positive first.