In Chapter 10 we defined torque τ for a rigid body that can rotate around a fixed axis, with each particle in the body forced to move in a path that is a circle centered on that axis. We now expand the definition of torque to apply it to an individual particle that moves along any path relative to a fixed point (rather than a fixed axis). The path need no longer be a circle, and we must write the torque as a vector 
that may have any direction.
Figure 11-10a shows such a particle at point A in an xy plane. A single force 
in that plane acts on the particle, and the particle’s position relative to the origin O is given by position vector 
. The torque acting on the particle relative to the fixed point O is a vector quantity defined as
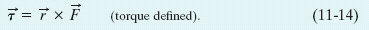
We can evaluate the vector (or cross) product in this definition of by using the rules for such products given in Section 3-8. To find the direction of , we slide the vector (without changing its direction) until its tail is at the origin O, so that the two vectors in the vector product are tail to tail as in Fig. 11-10b. We then use the right-hand rule for vector products in Fig. 3-20a, sweeping the fingers of the right hand from (the first vector in the product) into (the second vector). The outstretched right thumb then gives the direction of . In Fig. 11-10b, the direction of is in the positive direction of the z axis.
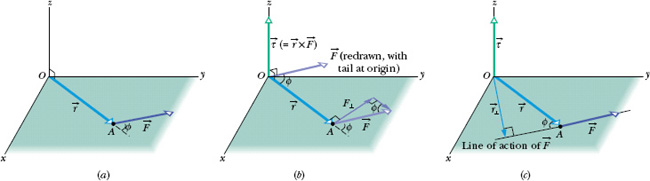
Fig. 11-10 Defining torque. (a) A force , lying in an xy plane, acts on a particle at point A. (b) This force produces a torque (= × ) on the particle with respect to the origin O. By the right-hand rule for vector (cross) products, the torque vector points in the positive direction of z. Its magnitude is given by rF⊥ in (b) and by r⊥ F in (c).
To determine the magnitude of , we apply the general result of Eq. 3-27 (c = ab sin 
), finding
where is the smaller angle between the directions of and when the vectors are tail to tail. From Figure 11-10b, we see that Eq. 11-15 can be rewritten as
where F⊥ (= F sin ) is the component of perpendicular to . From Fig. 11-10c, we see that Eq. 11-15 can also be rewritten as
where r⊥ (= r sin ) is the moment arm of (the perpendicular distance between O and the line of action of ).
In Fig. 11-11a, three forces, each of magnitude 2.0 N, act on a particle. The particle is in the xz plane at point A given by position vector , where r = 3.0 m and θ = 30°. Force 1 is parallel to the x axis, force 2 is parallel to the z axis, and force 3 is parallel to the y axis. What is the torque, about the origin O, due to each force?
Solution: The Key Idea here is that, because the three force vectors do not lie in a plane, we cannot evaluate their torques as in Chapter 10. Instead, we must use vector (or cross) products, with magnitudes given by Eq. 11-15 (τ = rF sin ) and directions given by the right-hand rule for vector products.
Because we want the torques with respect to the origin O, the vector required for each cross product is the given position vector. To determine the angle between the direction of and the direction of each force, we shift the force vectors of Fig. 11-11a, each in turn, so that their tails are at the origin. Figures 11-11b, c, and d, which are direct views of the xz plane, show the shifted force vectors 1, 2, and 3, respectively. (Note how much easier the angles are to see.) In Fig. 11-11d, the angle between the directions of and 3 is 90° and the symbol 
means 3 is directed into the page. If it were directed out of the page, it would be represented with the symbol 
.
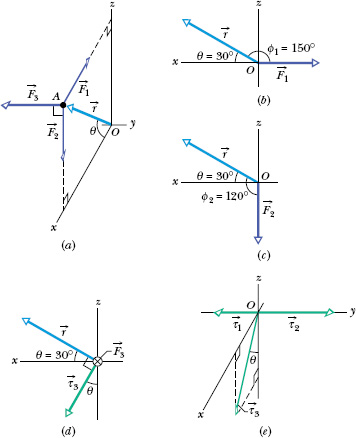
Fig. 11-11 (a) A particle at point A is acted on by three forces, each parallel to a coordinate axis. The angle (used in finding torque) is shown (b) for 1 and (c) for 2. (d) Torque 3 is perpendicular to both and 3 (force 3 is directed into the plane of the figure). (e) The torques (relative to the origin O) acting on the particle
Now, applying Eq. 11-15 for each force, we find the magnitudes of the torques to be
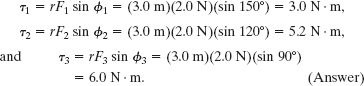
To find the directions of these torques, we use the righthand rule, placing the fingers of the right hand so as to rotate into through the smaller of the two angles between their directions. The thumb points in the direction of the torque. Thus 1 is directed into the page in Fig. 11-11b; 2 is directed out of the page in Fig. 11-11c; and 3 is directed as shown in Fig. 11-11d. All three torque vectors are shown in Fig. 11-11e.
CHECKPOINT 3 The position vector of a particle points along the positive direction of a z axis. If the torque on the particle is (a) zero, (b) in the negative direction of x, and (c) in the negative direction of y, in what direction is the force producing the torque?
PROBLEM – SOLVING TACTICS
TACTIC 1: Vector Products and Torques
Equation 11-15 for torques is our first application of the vector (or cross) product. You might want to review Section 3-8, where the rules for the vector product are given. In that section, Problem-Solving Tactic 5 lists many common errors in finding the direction of a vector product.
Keep in mind that a torque is calculated with respect to (or about) a point, which must be known if the value of the torque is to be meaningful. Changing the point can change the torque in both magnitude and direction. For example, in Sample Problem 11-3, the torques due to the three forces are calculated about the origin O. You can show that the torques due to the same three forces are all zero if they are calculated about point A (at the position of the particle), because then r = 0 for each force.
Leave a Reply