We wish to examine the rotation of a rigid body about a fixed axis. A rigid body is a body that can rotate with all its parts locked together and without any change in its shape. A fixed axis means that the rotation occurs about an axis that does not move. Thus, we shall not examine an object like the Sun, because the parts of the Sun (a ball of gas) are not locked together. We also shall not examine an object like a bowling ball rolling along a lane, because the ball rotates about a moving axis (the ball’s motion is a mixture of rotation and translation).
Figure 10-2 shows a rigid body of arbitrary shape in rotation about a fixed axis, called the axis of rotation or the rotation axis. In pure rotation (angular motion), every point of the body moves in a circle whose center lies on the axis of rotation, and every point moves through the same angle during a particular time interval. In pure translation (linear motion), every point of the body moves in a straight line, and every point moves through the same linear distance during a particular time interval. (Comparisons between angular and linear motion will appear throughout this chapter.)
We deal now—one at a time—with the angular equivalents of the linear quantities position, displacement, velocity, and acceleration.
Angular Position
Figure 10-2 shows a reference line, fixed in the body, perpendicular to the rotation axis and rotating with the body. The angular position of this line is the angle of the line relative to a fixed direction, which we take as the zero angular position. In Fig. 10-3, the angular position θ is measured relative to the positive direction of the x axis. From geometry, we know that θ is given by
Here s is the length of a circular arc that extends from the x axis (the zero angular position) to the reference line, and r is the radius of the circle.
An angle defined in this way is measured in radians (rad) rather than in revolutions (rev) or degrees. The radian, being the ratio of two lengths, is a pure number and thus has no dimension. Because the circumference of a circle of radius r is 2πr, there are 2π radians in a complete circle:
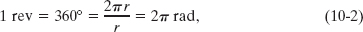
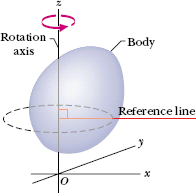
Fig. 10-2 A rigid body of arbitrary shape in pure rotation about the z axis of a coordinate system. The position of the reference line with respect to the rigid body is arbitrary, but it is perpendicular to the rotation axis. It is fixed in the body and rotates with the body.
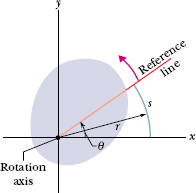
Fig. 10-3 The rotating rigid body of Fig. 10-2 in cross section, viewed from above. The plane of the cross section is perpendicular to the rotation axis, which now extends out of the page, toward you. In this position of the body, the reference line makes an angle θ with the x axis.
and thus
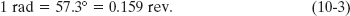
We do not reset θ to zero with each complete rotation of the reference line about the rotation axis. If the reference line completes two revolutions from the zero angular position, then the angular position θ of the line is θ = 4π rad.
For pure translation along an x axis, we can know all there is to know about a moving body if we know x(t), its position as a function of time. Similarly, for pure rotation, we can know all there is to know about a rotating body if we know θ(t), the angular position of the body’s reference line as a function of time.
Angular Displacement
If the body of Fig. 10-3 rotates about the rotation axis as in Fig. 10-4, changing the angular position of the reference line from θ1 to θ2, the body undergoes an angular displacement Δθ given by
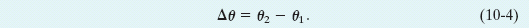
This definition of angular displacement holds not only for the rigid body as a whole but also for every particle within that body because the particles are all locked together.
If a body is in translational motion along an x axis, its displacement Δx is either positive or negative, depending on whether the body is moving in the positive or negative direction of the axis. Similarly, the angular displacement Δθ of a rotating body is either positive or negative, according to the following rule:
An angular displacement in the counterclockwise direction is positive, and one in the clockwise direction is negative.
The phrase “clocks are negative” can help you remember this rule (they certainly are negative when their alarms sound off early in the morning).
Angular Velocity
Suppose that our rotating body is at angular position θ1 at time t1 and at angular position θ2 at time t2 as in Fig. 10-4. We define the average angular velocity of the body in the time interval Δt from t1 to t2 to be
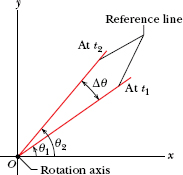
Fig. 10-4 The reference line of the rigid body of Figs. 10-2 and 10-3 is at angular position θ1 at time t1 and at angular position θ2 at a later time t2. The quantity Δθ (= θ2 − θ1) is the angular displacement that occurs during the interval Δt (= t2 − t1).
The body itself is not shown.
in which Δθ is the angular displacement that occurs during Δt (ω is the lowercase Greek letter omega).
The (instantaneous) angular velocity ω, with which we shall be most concerned, is the limit of the ratio in Eq. 10-5 as Δt approaches zero. Thus,
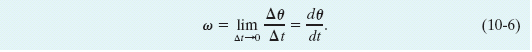
If we know θ(t), we can find the angular velocity ω by differentiation.
Equations 10-5 and 10-6 hold not only for the rotating rigid body as a whole but also for every particle of that body because the particles are all locked together. The unit of angular velocity is commonly the radian per second (rad/s) or the revolution per second (rev/s). Another measure of angular velocity was used during at least the first three decades of rock: Music was produced by vinyl (phonograph) records that were played on turntables at “
rpm” or “45 rpm,” meaning at rev/min or 45 rev/min.
If a particle moves in translation along an x axis, its linear velocity ν is either positive or negative, depending on whether the particle is moving in the positive or negative direction of the axis. Similarly, the angular velocity ω of a rotating rigid body is either positive or negative, depending on whether the body is rotating counterclockwise (positive) or clockwise (negative). (“Clocks are negative” still works.) The magnitude of an angular velocity is called the angular speed, which is also represented with ω.
Angular Acceleration
If the angular velocity of a rotating body is not constant, then the body has an angular acceleration. Let ω2 and ω1 be its angular velocities at times t2 and t1, respectively. The average angular acceleration of the rotating body in the interval from t1 to t2 is defined as
in which Δω is the change in the angular velocity that occurs during the time interval Δt. The (instantaneous) angular acceleration α, with which we shall be most concerned, is the limit of this quantity as Δt approaches zero. Thus,
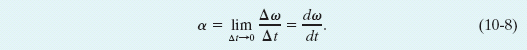
Equations 10-7 and 10-8 also hold for every particle of that body. The unit of angular acceleration is commonly the radian per second-squared (rad/s2) or the revolution per second-squared (rev/s2).
The disk in Fig. 10-5a is rotating about its central axis like a merry-go-round. The angular position θ(t) of a reference line on the disk is given by
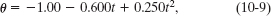
with t in seconds, θ in radians, and the zero angular position as indicated in the figure.
(a) Graph the angular position of the disk versus time from t = −3.0 s to t = 5.4 s. Sketch the disk and its angular position reference line at t = −2.0 s, 0 s, and 4.0 s, and when the curve crosses the t axis.
Solution: The Key Idea here is that the angular position of the disk is the angular position θ(t) of its reference line, which is given by Eq. 10-9 as a function of time. So we graph Eq. 10-9; the result is shown in Fig. 10-5b.
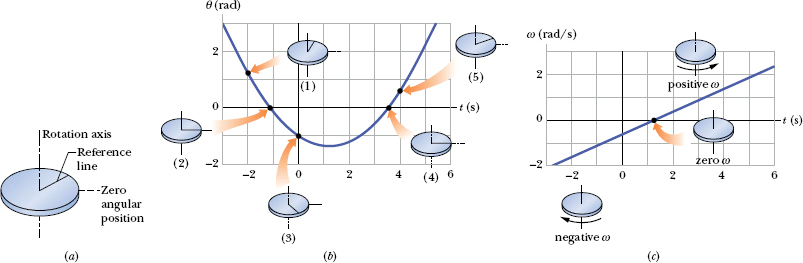
Fig. 10-5 (a) A rotating disk. (b) A plot of the disk’s angular position θ(t). Five sketches indicate the angular position of the reference line on the disk for five points on the curve. (c) A plot of the disk’s angular velocity ω(t). Positive values of ω correspond to counterclockwise rotation, and negative values to clockwise rotation.
To sketch the disk and its reference line at a particular time, we need to determine θ for that time. To do so, we substitute the time into Eq. 10-9. For t = −2.0 s, we get
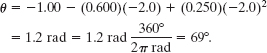
This means that at t = −2.0 s the reference line on the disk is rotated counterclockwise from the zero position by 1.2 rad = 69° (counterclockwise because θ is positive). Sketch 1 in Fig. 10-5b shows this position of the reference line.
Similarly, for t = 0, we find θ = −1.00 rad = −57°, which means that the reference line is rotated clockwise from the zero angular position by 1.0 rad, or 57°, as shown in sketch 3. For t = 4.0 s, we find θ = 0.60 rad = 34° (sketch 5). Drawing sketches for when the curve crosses the t axis is easy, because then θ = 0 and the reference line is momentarily aligned with the zero angular position (sketches 2 and 4).
(b) At what time tmin does θ(t) reach the minimum value shown in Fig. 10-5b? What is that minimum value?
Solution: The Key Idea here is that to find the extreme value (here the minimum) of a function, we take the first derivative of the function and set the result to zero. The first derivative of θ(t) is
Setting this to zero and solving for t give us the time at which θ(t) is minimum:
To get the minimum value of θ, we next substitute tmin into Eq. 10-9, finding
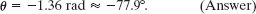
This minimum of θ(t) (the bottom of the curve in Fig. 10-5b) corresponds to the maximum clockwise rotation of the disk from the zero angular position, somewhat more than is shown in sketch 3.
(c) Graph the angular velocity ω of the disk versus time from t = −3.0 s to t = 6.0 s. Sketch the disk and indicate the direction of turning and the sign of ω at t = −2.0 s, 4.0 s, and tmin.
Solution: The Key Idea here is that, from Eq. 10-6, the angular velocity ω is equal to dθ/dt as given in Eq. 10-10. So, we have
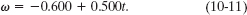
The graph of this function ω(t) is shown in Fig. 10-5c.
To sketch the disk at t = −2.0 s, we substitute that value into Eq. 10-11, obtaining
The minus sign tells us that at t = −2.0 s, the disk is turning clockwise, as suggested by the lowest sketch in Fig. 10-5c.
Substituting t = 4.0 s into Eq. 10-11 gives us
The implied plus sign tells us that at t = 4.0 s, the disk is turning counterclockwise (the highest sketch in Fig. 10-5c).
For tmin, we already know that dθ/dt = 0. So, we must also have ω = 0. That is, the disk momentarily stops when the reference line reaches the minimum value of θ in Fig. 10-5b, as suggested by the center sketch in Fig. 10-5c.
(d) Use the results in parts (a) through (c) to describe the motion of the disk from t = −3.0 s to t = 6.0 s.
Solution: When we first observe the disk at t = −3.0 s, it has a positive angular position and is turning clockwise but slowing. It stops at angular position θ = −1.36 rad and then begins to turn counterclockwise, with its angular position eventually becoming positive again.
CHECK POINT 1 A disk can rotate about its central axis like the one in Fig. 10-5a. Which of the following pairs of values for its initial and final angular positions, respectively, give a negative angular displacement: (a) −3 rad, +5 rad, (b) −3 rad, −7 rad, (c) 7 rad, −3 rad?
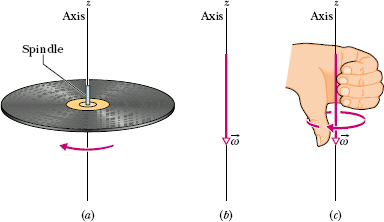
Fig. 10-6 (a) A record rotating about a vertical axis that coincides with the axis of the spindle. (b) The angular velocity of the rotating record can be represented by the vector 
, lying along the axis and pointing down, as shown. (c) We establish the direction of the angular velocity vector as downward by using a right-hand rule. When the fingers of the right hand curl around the record and point the way it is moving, the extended thumb points in the direction of .
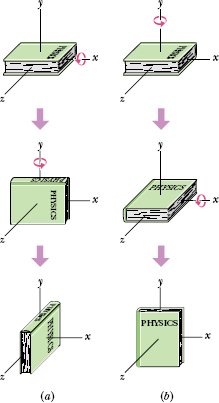
Fig. 10-7 (a) From its initial position, at the top, the book is given two successive 90° rotations, first about the (horizontal) x axis and then about the (vertical) y axis. (b) The book is given the same rotations, but in the reverse order.
Leave a Reply