Now that we have defined linear momentum for a single particle, let us extend the definition to a system of particles. Consider a system of n particles, each with its own mass, velocity, and linear momentum. The particles may interact with each other, and external forces may act on them as well. The system as a whole has a total linear momentum 
, which is defined to be the vector sum of the individual particles’ linear momenta. Thus,
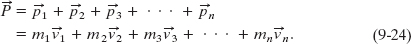
If we compare this equation with Eq. 9-17, we see that
which is another way to define the linear momentum of a system of particles:
The linear momentum of a system of particles is equal to the product of the total mass M of the system and the velocity of the center of mass.
If we take the time derivative of Eq. 9-25, we find
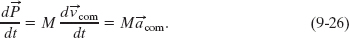
Comparing Eqs. 9-14 and 9-26 allows us to write Newton’s second law for a system of particles in the equivalent form
where 
is the net external force acting on the system. This equation is the generalization of the single-particle equation 
to a system of many particles. In words, the equation says that the net external force on a system of particles changes the linear momentum 
of the system. Conversely, the linear momentum can be changed only by a net external force. If there is no net external force, cannot change.
The collision of a ball with a bat collapses part of the ball.
Leave a Reply