The Kinetic Energy of Rolling

Let us now calculate the kinetic energy of the rolling wheel as measured by the stationary observer. If we view the rolling as pure rotation about an axis through P in Fig. 11-6, then from Eq. 10-34 we have

in which ω is the angular speed of the wheel and I_P is the rotational inertia of the wheel about the axis through P. From the parallel-axis theorem of Eq. 10-36 (I = I_com + Mh²), we have

in which M is the mass of the wheel, I_com is its rotational inertia about an axis through its center of mass, and R (the wheel’s radius) is the perpendicular distance h. Substituting Eq. 11-4 into Eq. 11-3, we obtain

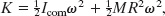
and using the relation v_com = ωR (Eq. 11-2) yields

We can interpret the term  as the kinetic energy associated with the rotation of the wheel about an axis through its center of mass (Fig. 11-4a), and the term  as the kinetic energy associated with the translational motion of the wheel’s center of mass (Fig. 11-4b). Thus, we have the following rule:

 A rolling object has two types of kinetic energy: a rotational kinetic energy  due to its rotation about its center of mass and a translational kinetic energy  due to translation of its center of mass.

Sample Problem 11-1

Approximate each wheel on the car Thrust SSC as a disk of uniform thickness and mass M = 170 kg, and assume smooth rolling. When the car’s speed was 1233 km/h, what was the kinetic energy of each wheel?

Solution: Equation 11-5 gives the kinetic energy of a rolling object, but we need three Key Ideas to use it:

1. When we speak of the speed of a rolling object, we always mean the speed of the center of mass, so here v_com = 1233 km/h = 342.5 m/s.

2. Equation 11-5 requires the angular speed ω of the rolling object, which we can relate to v_com with Eq. 11-2, writing ω = v_com/R, where R is the wheel’s radius.

3. Equation 11-5 also requires the rotational inertia I_com of the object about its center of mass. From Table 10-2c, we find that, for a uniform disk, .

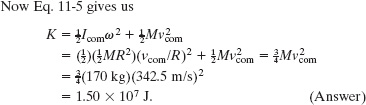
(Note that the wheel’s radius R cancels out of the calculation.)

This answer gives one measure of the danger when the land-speed record was set by Thrust SSC: The kinetic energy of each (cast aluminum) wheel on the car was huge, almost as much as the kinetic energy (2.1 × 10⁷ J) of the spinning steel disk that exploded in Sample Problem 10-7. Had a wheel hit any hard obstacle along the car’s path, the wheel would have exploded the way the steel disk did, with the car and driver moving faster than sound!