Friction and Rolling
If a wheel rolls at constant speed, as in Fig. 11-3, it has no tendency to slide at the point of contact P, and thus no frictional force acts there. However, if a net force acts on the rolling wheel to speed it up or to slow it, then that net force causes acceleration ![]() of the center of mass along the direction of travel. It also causes the wheel to rotate faster or slower, which means it causes an angular acceleration α. These accelerations tend to make the wheel slide at P. Thus, a frictional force must act on the wheel at P to oppose that tendency.
of the center of mass along the direction of travel. It also causes the wheel to rotate faster or slower, which means it causes an angular acceleration α. These accelerations tend to make the wheel slide at P. Thus, a frictional force must act on the wheel at P to oppose that tendency.
If the wheel does not slide, the force is a static frictional force ![]() and the motion is smooth rolling. We can then relate the magnitudes of the linear acceleration
and the motion is smooth rolling. We can then relate the magnitudes of the linear acceleration ![]() and the angular acceleration α by differentiating Eq. 11-2 with respect to time (with R held constant). On the left side, dvcom/dt is acom, and on the right side dω/dt is α. So, for smooth rolling we have
and the angular acceleration α by differentiating Eq. 11-2 with respect to time (with R held constant). On the left side, dvcom/dt is acom, and on the right side dω/dt is α. So, for smooth rolling we have
If the wheel does slide when the net force acts on it, the frictional force that acts at P in Fig. 11-3 is a kinetic frictional force ![]() . The motion then is not smooth rolling, and Eq. 11-6 does not apply to the motion. In this chapter we discuss only smooth rolling motion.
. The motion then is not smooth rolling, and Eq. 11-6 does not apply to the motion. In this chapter we discuss only smooth rolling motion.
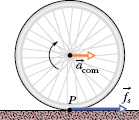
Fig. 11-7 A wheel rolls horizontally without sliding while accelerating with linear acceleration ![]() . A static frictional force
. A static frictional force ![]() acts on the wheel at P, opposing its tendency to slide.
acts on the wheel at P, opposing its tendency to slide.
Figure 11-7 shows an example in which a wheel is being made to rotate faster while rolling to the right along a flat surface, as on a bicycle at the start of a race. The faster rotation tends to make the bottom of the wheel slide to the left at point P. A frictional force at P, directed to the right, opposes this tendency to slide. If the wheel does not slide, that frictional force is a static frictional force ![]() (as shown), the motion is smooth rolling, and Eq. 11-6 applies to the motion.(Without friction, bicycle races would be stationary and very boring.)
(as shown), the motion is smooth rolling, and Eq. 11-6 applies to the motion.(Without friction, bicycle races would be stationary and very boring.)
If the wheel in Fig. 11-7 were made to rotate slower, as on a slowing bicycle, we would change the figure in two ways: The directions of the center-of-mass acceleration ![]() and the frictional force
and the frictional force ![]() at point P would now be to the left.
at point P would now be to the left.
Rolling Down a Ramp
Figure 11-8 shows a round uniform body of mass M and radius R rolling smoothly down a ramp at angle θ, along an x axis. We want to find an expression for the body’s acceleration acom,x down the ramp. We do this by using Newton’s second law in both its linear version (Fnet = Ma) and its angular version (τnet = Iα).
We start by drawing the forces on the body as shown in Fig. 11-8:
1. The gravitational force ![]() on the body is directed downward. The tail of the vector is placed at the center of mass of the body. The component along the ramp is Fg sin θ, which is equal to Mg sin θ.
on the body is directed downward. The tail of the vector is placed at the center of mass of the body. The component along the ramp is Fg sin θ, which is equal to Mg sin θ.
2. A normal force ![]() is perpendicular to the ramp. It acts at the point of contact P, but in Fig. 11-8 the vector has been shifted along its direction until its tail is at the body’s center of mass.
is perpendicular to the ramp. It acts at the point of contact P, but in Fig. 11-8 the vector has been shifted along its direction until its tail is at the body’s center of mass.
3. A static frictional force ![]() acts at the point of contact P and is directed up the ramp. (Do you see why? If the body were to slide at P, it would slide down the ramp. Thus, the frictional force opposing the sliding must be up the ramp.)
acts at the point of contact P and is directed up the ramp. (Do you see why? If the body were to slide at P, it would slide down the ramp. Thus, the frictional force opposing the sliding must be up the ramp.)
We can write Newton’s second law for components along the x axis in Fig. 11-8 (F net,x = max) as

This equation contains two unknowns, fs and acom,x. (We should not assume that fs is at its maximum value fs,max. All we know is that the value of fs is just right for the body to roll smoothly down the ramp, without sliding.)
We now wish to apply Newton’s second law in angular form to the body’s rotation about its center of mass. First, we shall use Eq. 10-41 (τ = r⊥F) to write the torques on the body about that point. The frictional force ![]() has moment arm R and thus produces a torque Rfs, which is positive because it tends to rotate the body counterclockwise in Fig. 11-8. Forces
has moment arm R and thus produces a torque Rfs, which is positive because it tends to rotate the body counterclockwise in Fig. 11-8. Forces ![]() and
and ![]() have zero moment arms about the center of mass and thus produce zero torques. So we can write the angular form of Newton’s second law (τnet = Iα) about an axis through the body’s center of mass as
have zero moment arms about the center of mass and thus produce zero torques. So we can write the angular form of Newton’s second law (τnet = Iα) about an axis through the body’s center of mass as

This equation contains two unknowns, fs and α.
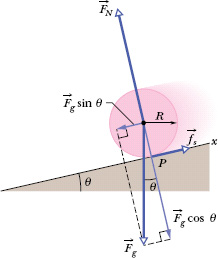
Fig. 11-8 A round uniform body of radius R rolls down a ramp. The forces that act on it are the gravitational force ![]() , a normal force
, a normal force ![]() , and a frictional force
, and a frictional force ![]() pointing up the ramp. (For clarity, vector
pointing up the ramp. (For clarity, vector ![]() has been shifted in the direction it points until its tail is at the center of the body.)
has been shifted in the direction it points until its tail is at the center of the body.)
Because the body is rolling smoothly, we can use Eq. 11-6 (acom = αR) to relate the unknowns acom,x and α. But we must be cautious because here acom,x is negative (in the negative direction of the x axis) and α is positive (counterclockwise). Thus we substitute −acom,x/R for α in Eq. 11-8. Then, solving for fs, we obtain

Substituting the right side of Eq. 11-9 for fs in Eq. 11-7, we then find
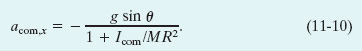
We can use this equation to find the linear acceleration acom,x of any body rolling along an incline of angle θ with the horizontal.
![]() CHECKPOINT 2 Disks A and B are identical and roll across a floor with equal speeds. Then disk A rolls up an incline, reaching a maximum height h, and disk B moves up an incline that is identical except that it is frictionless. Is the maximum height reached by disk B greater than, less than, or equal to h?
CHECKPOINT 2 Disks A and B are identical and roll across a floor with equal speeds. Then disk A rolls up an incline, reaching a maximum height h, and disk B moves up an incline that is identical except that it is frictionless. Is the maximum height reached by disk B greater than, less than, or equal to h?
A uniform ball, of mass M = 6.00 kg and radius R, rolls smoothly from rest down a ramp at angle θ = 30.0° (Fig. 11-8).
(a) The ball descends a vertical height h = 1.20 m to reach the bottom of the ramp. What is its speed at the bottom?
Solution: One Key Idea here is that we can relate the ball’s speed at the bottom to its kinetic energy Kf there. A second Key Idea is that the mechanical energy E of the ball–Earth system is conserved as the ball rolls down the ramp. The reason is that the only force doing work on the ball is the gravitational force, a conservative force. The normal force on the ball from the ramp does zero work because it is perpendicular to the ball’s path. The frictional force on the ball from the ramp does not transfer any energy to thermal energy because the ball does not slide (it rolls smoothly).
Therefore, we can write the conservation of mechanical energy (Ef = Ei) as
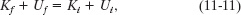
where subscripts f and i refer to the final values (at the bottom) and initial values (at rest), respectively. The gravitational potential energy is initially Ui = Mgh (where M is the ball’s mass) and finally Uf = 0. The kinetic energy is initially Ki = 0. For the final kinetic energy Kf, we need a third Key Idea: Because the ball rolls, the kinetic energy involves both translation and rotation, so we include them both by using the right side of Eq. 11-5. Substituting all these expressions into Eq. 11-11 gives us
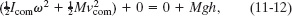
where Icom is the ball’s rotational inertia about an axis through its center of mass, vcom is the requested speed at the bottom, and ω is the angular speed there.
Because the ball rolls smoothly, we can use Eq. 11-2 to substitute vcom/R for ω to reduce the unknowns in Eq. 11-12. Doing so, substituting ![]() for Icom (from Table 10-2f), and then solving for vcom give us
for Icom (from Table 10-2f), and then solving for vcom give us
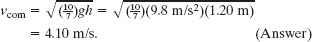
Note that the answer does not depend on the mass M or radius R of the ball.
(b) What are the magnitude and direction of the frictional force on the ball as it rolls down the ramp?
Solution: The Key Idea here is that, because the ball rolls smoothly, Eq. 11-9 gives the frictional force on the ball. However, first we need the ball’s acceleration acom,x from Eq. 11-10:
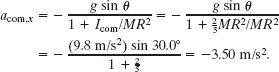
Note that we needed neither mass M nor radius R to find acom,x. Thus, any size ball with any uniform mass would have this acceleration down a 30.0° ramp, provided the ball rolls smoothly.
We can now solve Eq. 11-9 as
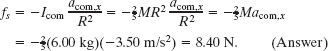
Note that we needed mass M but not radius R. Thus, the frictional force on any 6.00 kg ball rolling smoothly down a 30.0° ramp would be 8.40 N regardless of the ball’s radius.
Leave a Reply