The Angular Momentum of a System of Particles

Now we turn our attention to the angular momentum of a system of particles with respect to an origin. The total angular momentum  of the system is the (vector) sum of the angular momenta  of the individual particles (here with label i):

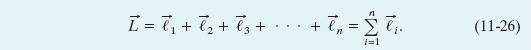
With time, the angular momenta of individual particles may change, either because of interactions within the system (between the individual particles) or because of influences that may act on the system from the outside. We can find the resulting change in  by taking the time derivative of Eq. 11-26. Thus,

From Eq. 11-23, we see that  is equal to the net torque on the  on the ith particle. We can rewrite Eq. 11-27 as

That is, the rate of change of the system’s angular momentum  is equal to the vector sum of the torques on its individual particles. Those torques include internal torques (due to forces between the particles) and external torques (due to forces on the particles from bodies external to the system). However, the forces between the particles always come in third-law force pairs so their torques sum to zero. Thus, the only torques that can change the total angular momentum  of the system are the external torques acting on the system.

Let  represent the net external torque, the vector sum of all external torques on all particles in the system. Then we can write Eq. 11-28 as

which is Newton’s second law in angular form. It says:

 The net external torque  acting on a system of particles is equal to the time rate of change of the system’s total angular momentum .

Equation 11-29 is analogous to  (Eq. 9-23) but requires extra caution: Torques and the system’s angular momentum must be measured relative to the same origin. If the center of mass of the system is not accelerating relative to an inertial frame, that origin can be any point. However, if the center of mass of the system is accelerating, the origin can be only at that center of mass. As an example, consider a wheel as the system of particles. If the wheel is rotating about an axis that is fixed relative to the ground, then the origin for applying Eq. 11-29 can be any point that is stationary relative to the ground. However, if the wheel is rotating about an axis that is accelerating (such as when the wheel rolls down a ramp), then the origin can be only at the wheel’s center of mass.