The Angular Momentum of a Rigid Body Rotating About a Fixed Axis

We next evaluate the angular momentum of a system of particles that form a rigid body that rotates about a fixed axis. Figure 11-15a shows such a body. The fixed axis of rotation is a z axis, and the body rotates about it with constant angular speed ω. We wish to find the angular momentum of the body about that axis.

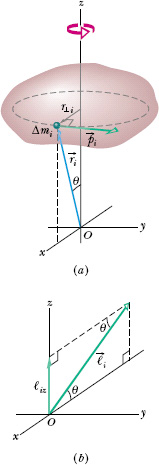
Fig. 11-15   (a) A rigid body rotates about a z axis with angular speed ω. A mass element of mass Δm_i within the body moves about the z axis in a circle with radius r_⊥i. The mass element has linear momentum _i, and it is located relative to the origin O by position vector _i. Here the mass element is shown when r_⊥i is parallel to the x axis. (b) The angular momentum _i, with respect to O, of the mass element in (a). The z component ℓ_iz is also shown.

We can find the angular momentum by summing the z components of the angular momenta of the mass elements in the body. In Fig. 11-15a, a typical mass element, of mass Δm_i, moves around the z axis in a circular path. The position of the mass element is located relative to the origin O by position vector _i. The radius of the mass element’s circular path is r_⊥i, the perpendicular distance between the element and the z axis.

The magnitude of the angular momentum _i of this mass element, with respect to O, is given by Eq. 11-19:

ℓ_i = (r_i)(p_i)(sin 90°) = (r_i)(Δm_i v_i),

where p_i and v_i are the linear momentum and linear speed of the mass element, and 90° is the angle between _i and _i. The angular momentum vector _i for the mass element in Fig. 11-15a is shown in Fig. 11-15b; its direction must be perpendicular to those of _i and _i.

We are interested in the component of _i that is parallel to the rotation axis, here the z axis. That z component is

ℓ_iz = ℓ_i sin θ = (r_i sin θ)(Δm_i v_i) = r_⊥i Δm_i v_i.

The z component of the angular momentum for the rotating rigid body as a whole is found by adding up the contributions of all the mass elements that make up the body. Thus, because v = ωr_⊥, we may write

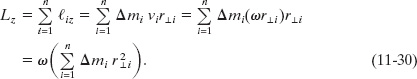
We can remove ω from the summation here because it has the same value for all points of the rotating rigid body.

The quantity  in Eq. 11-30 is the rotational inertia I of the body about the fixed axis (see Eq. 10-33). Thus Eq. 11-30 reduces to

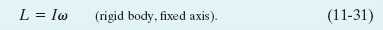
We have dropped the subscript z, but you must remember that the angular momentum defined by Eq. 11-31 is the angular momentum about the rotation axis. Also, I in that equation is the rotational inertia about that same axis.

Table 11-1, which supplements Table 10-3, extends our list of corresponding linear and angular relations.

TABLE 11-1   More Corresponding Variables and Relations for Translational and Rotational Motion^a

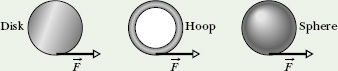
CHECKPOINT 6   In the figure, a disk, a hoop, and a solid sphere are made to spin about fixed central axes (like a top) by means of strings wrapped around them, with the strings producing the same constant tangential force  on all three objects. The three objects have the same mass and radius, and they are initially stationary. Rank the objects according to (a) their angular momentum about their central axes and (b) their angular speed, greatest first, when the strings have been pulled for a certain time t.

Sample Problem 11-6

George Washington Gale Ferris, Jr., a civil engineering graduate from Rensselaer Polytechnic Institute, built the original Ferris wheel (Fig. 11-16) for the 1893 World’s Columbian Exposition in Chicago. The wheel, an astounding engineering construction at the time, carried 36 wooden cars, each holding as many as 60 passengers, around a circle of radius R = 38 m. The mass of each car was about 1.1 × 10⁴ kg. The mass of the wheel’s structure was about 6.0 × 10⁵ kg, which was mostly in the circular grid from which the cars were suspended. The wheel made a complete rotation at an angular speed ω_F in about 2 min.

(a) Estimate the magnitude L of the angular momentum of the wheel and its passengers while the wheel rotated at ω_F.

Solution: The Key Idea here is that we can treat the wheel, cars, and passengers as a rigid object rotating about a fixed axis, at the wheel’s axle. Then Eq. 11-31 (L = Iω) gives the magnitude of the angular momentum of that object. We need to find ω_F and the rotational inertia I of this object.

To find I, let us start with the loaded cars. Because we can treat them as particles, at distance R from the axis of rotation, we know from Eq. 10-33 that their rotational inertia is I_pc = M_pcR², where M_pc is their total mass. Let us assume that the 36 cars are each filled with 60 passengers, each of mass 70 kg. Then their total mass is

M_pc = 36[1.1 × 10⁴ kg + 60(70 kg)] = 5.47 × 10⁵ kg

and their rotational inertia is

I_pc = M_pcR² = (5.47 × 10⁵ kg)(38 m)² = 7.90 × 10⁸ kg · m².

Next we consider the structure of the wheel. Let us assume that the rotational inertia of the structure is due mainly to the circular grid suspending the cars. Further, let us assume that the grid forms a hoop of radius R, with a mass M_hoop of 3.0 × 10⁵ kg (half the wheel’s mass). From Table 10-2a, the rotational inertia of the hoop is

I_hoop = M_hoopR² = (3.0 × 10⁵ kg)(38 m)²
         = 4.33 × 10⁸ kg · m².

The combined rotational inertia I of the cars, passengers, and hoop is then

I = I_pc + I_hoop = 7.90 × 10⁸ kg · m² + 4.33 × 10⁸ kg · m²
  = 1.22 × 10⁹ kg · m².

To find the rotational speed ω_F, we use Eq. 10-5 (ω_avg = Δθ/Δt). Here the wheel goes through an angular displacement of Δθ = 2π rad in a time period Δt = 2 min. Thus, we have

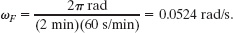
Fig. 11-16   The original Ferris wheel, built in 1893 near the University of Chicago, towered over the surrounding buildings.

Now we can find the magnitude L of the angular momentum with Eq. 11-31:

L = Iω_F = (1.22 × 10⁹ kg · m²)(0.0524 rad/s)
   = 6.39 × 10⁷ kg · m²/s ≈ 6.4 × 10⁷ kg · m²/s. (Answer)

(b) Assume that the fully loaded wheel is rotated from rest to ω_F in a time period Δt₁ = 5.0 s. What is the magnitude τ_avg of the average net external torque acting on it during Δt₁?

Solution: The Key Idea here is that the average net external torque is related to the change ΔL in the angular momentum of the loaded wheel by Eq. 11-29 . Because the wheel rotates about a fixed axis to reach angular speed ω_F in time period Δt₁, we can rewrite Eq. 11-29 as τ_avg = ΔL/Δt₁. The change ΔL is from zero to the answer for part (a). Thus, we have